| WEB版 現代数学入門講座 Vol. 1 (2009年8月14日) | ||||||||
|
掛谷問題ショートコース
|
||||||||
| 東京大学 新井仁之 (* 2018より早稲田大学) | ||||||||
|
本ページの文章,図版及び掲載写真の無断複写・転載を禁じます.リンクはフリーです.
|
||||||||
| 掛谷問題というのは,1916年(大正5年)11月に東北帝国大学の掛谷宗一博士により考えられた図形と面積に関する非常に面白い問題です.面白いだけでなく,現代解析学における重要なテーマともつながっています.ここでは掛谷問題とその発展について解説をしたいと思います. | ||||||||
| なお,第1章の掛谷問題のはじまりは,筆者の独自の調査により明らかにされたことです([2],[3])。 | ||||||||
| 2022/3/15追記:掛谷問題のはじまりから、最近の話題までの筆者による講義動画も公開されていますので,併せてご覧ください。 | ||||||||
| 数理科学デジタルオープンレクチャーズ 掛谷予想 全4作 | ||||||||
| No.1, No.2, No.3, No.4. | ||||||||
| 1章 古典的な意味での掛谷問題 | ||||||||
| 掛谷問題と呼ばれる問題には,古典的な意味の掛谷問題と,現代解析学における掛谷問題があります.まず古典的な意味での掛谷問題の解説から始めます.これは次のような問題です. | ||||||||
| 古典的な意味の掛谷問題 | ||||||||
| 「長さ 1 の線分を一回転させることのできる凸図形の中で,面積が最も小さくてすむものは何か?」 | ||||||||
| ここで凸図形とは次のように定義される図形です. | ||||||||
| 「ある図形Aが凸であるとは,A内の任意の二点を線分で結ぶとき,その線分もAの中に含まれることである」 | ||||||||
| たとえば円板は凸図形です.また正三角形や楕円なども凸図形です. | ||||||||
| さて,長さ1の線分を一回転させることのできる凸図形として,どのようなものが思い浮かびますか? | ||||||||
| すぐに思いつくのは,直径が1の円でしょう.この円板の中では次のように長さ1の線分を一回転させることができます | ||||||||
 |
||||||||
| 図1.直径1の円の中で長さ1の線分を回転できる. | ||||||||
| これは直径が1の円ですから,面積は (1/4)πでおよそ 0.7854 です.これよりも小さな図形はあると思いますか? | ||||||||
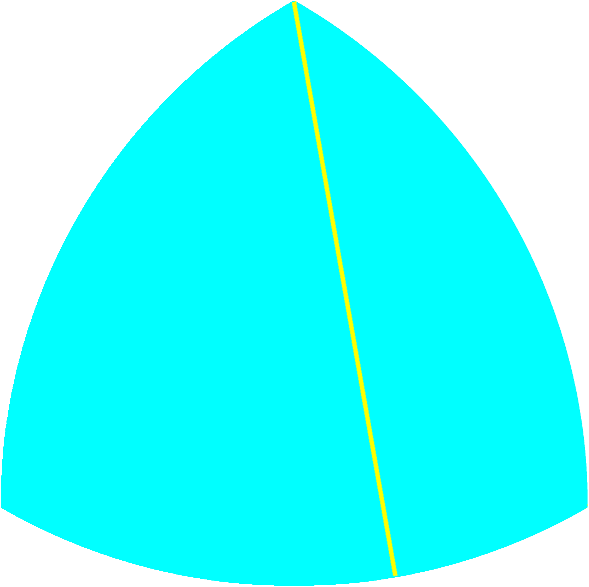
| 掛谷宗一は当初,掛谷問題の答えが次のルーローの三角形であると考えました.このことは掛谷直筆のノートに記されています. | ||||||||
 |
||||||||
| 図2.ルーローの三角形.この中でも長さ1の線分を回転できる. | ||||||||
 |
||||||||
| 図3.掛谷宗一直筆ノートより(統計数理研究所図書室の許可を得て撮影) | ||||||||
| ルーローの三角形の面積は (1/2)π-(1/2)√3 で,およそ 0.70478 です.これは確かに直径1の円の面積 (1/4)π よりも小さくなっています. | ||||||||
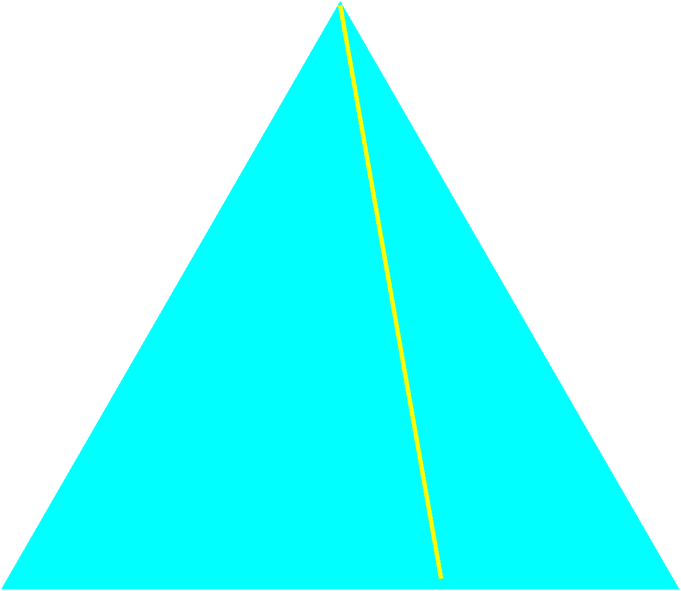
| しかし,掛谷がこの答えを考えたすぐ後に,掛谷の同僚であった藤原松三郎と窪田忠彦は,もっと小さい図形の中で長さ1の線分を一回転できることを掛谷に指摘しました.その図形というのは高さ1の正三角形です.その面積は 1/√3 です. | ||||||||
 |
||||||||
| 図4.高さが1の正三角形の中で,長さ1の線分が一回転できる. | ||||||||
| しかしこれよりも面積が小さいもので線分が一回転できるものがあるかどうかは,わかりませんでした.1916年11月末のことでした. | ||||||||
| それから5年後の1921年にJ.Palという人が,この藤原の考えた正三角形が掛谷問題をみたす面積最小の凸図形であることを証明しました. | ||||||||
| さて,窪田は凸という条件を外せば,もっと小さな面積の図形の中で長さ1の線分を回転させることができることを発見しました.それは次のような図形です. | ||||||||
 |
||||||||
| 図5.窪田の考えた図形.ただし凸ではない. | ||||||||
| 窪田の考えた図形は,次の方程式で記述される曲線で囲まれる図形となっています. | ||||||||
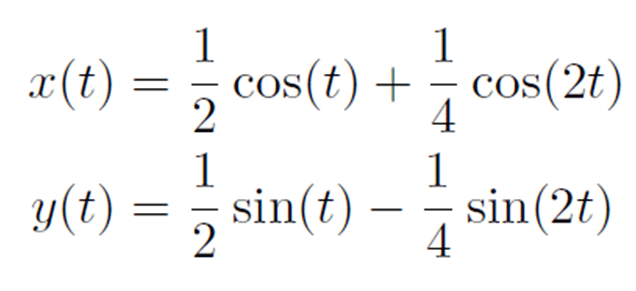 |
||||||||
| この図形の面積はπ/8 です. | ||||||||
| それでは,これらの図形の中でどのように長さ1の線分が一回転するのかをアニメーションで見てみましょう. | ||||||||
| アニメーション (ここをクリック) mp4版 | ||||||||
| swf版はこちら | ||||||||
| 2章 現代解析学における掛谷問題 | ||||||||
| 凸という条件を課さなければ,もっと小さいな面積の図形の中で,長さ1の線分が一回転できそうですね.このことは,ロシアの数学者であるベシコヴィッチが研究し,次のような驚くべき定理を証明しました. | ||||||||
| ベシコヴィッチの定理 (1928) | ||||||||
| どんな小さな正の数 εに対しても,面積がそれよりも小さい平面図形で,その中で長さ1の線分を回転させることができるようなものが存在する. | ||||||||
| じつはこの定理の証明をする前に,ベシコヴィッチは次のような不思議な定理も証明しています.上記のベシコヴィッチの定理は次の定理を用いて証明されました. | ||||||||
| ベシコヴィッチの定理 (1919) | ||||||||
| あらゆる方向の長さ 1 の線分を含み,かつ面積が 0 となるような平面図形 K が存在する. | ||||||||
| ベシコヴィッチの定理(1919)のような図形を想像することは難しいのではないかと思います.このような図形の作り方はいくつか知られています.ここではペロンの木という基本的なアイデアをアニメーションにしました.60度の範囲内の傾きをもつ長さ1の線分を含みながら,正三角形の面積が圧縮されていく様子がわかると思います. | ||||||||
| アニメーション(ここをクリック) mp4版 | ||||||||
| swf版はこちら | ||||||||
| さて,このベシコヴィッチの結果から,次のような集合が定義されました. | ||||||||
| 定義 (掛谷集合) | ||||||||
| 2 次元ユークリッド空間内の有界な閉集合 K で,あらゆる方向の長さ 1 の線分を含み,その面積が 0 となるようなものを 2 次元掛谷集合という. | ||||||||
| 一般に,d 次元ユークリッド空間内の有界な閉集合 K で,あらゆる方向の長さ 1 の線分を含み,そのd次元ルベーグ測度が 0 となるようなものを d 次元掛谷集合という. | ||||||||
| ところで,フラクタル幾何学に「ハウスドルフ次元」という概念があります.私たちは「次元」というと,たとえば点は0次元,線は1次元,面は2次元というものを思い浮かべます.ハウスドルフ次元は,より複雑な図形に対して定義されたもので,1.5次元だとか,2.4次元といったものもあります.これはフラクタル幾何学という分野でよく用いられる概念です.ハウスドルフ次元とフラクタル幾何については,後の講義で述べることにします.ハウスドルフ次元の定義を知りたい方は文献 [1] をご覧ください. | ||||||||
| 掛谷集合のハウスドルフ次元はどのようになっているでしょう? | ||||||||
| 1971年にデーヴィスが次のような定理を証明しています. | ||||||||
| デーヴィスの定理 (1971) | ||||||||
| 2 次元掛谷集合のハウスドルフ次元は 2 である. | ||||||||
| それでは 3 次元以上の場合はどうなっているでしょう.じつは,これはまだ解決していない問題なのです.この問題は現在,掛谷問題と呼ばれており,実解析の最も有名な問題の一つとして,研究者の間では広く知られています. | ||||||||
| 掛谷問題 | ||||||||
| d 次元掛谷集合 (d>;2) のハウスドルフ次元は何か? | ||||||||
| d次元掛谷集合のハウスドルフ次元は d であるというのが大方の予想で,これは通常,掛谷予想と呼ばれています. | ||||||||
| 掛谷問題,掛谷予想は,解析学の多くの未解決問題と関連していることが,Taoらによって証明されています( [1], [2] 参照). | ||||||||
| 学習用文献 | ||||||||
| [1] 新井仁之,ルベーグ積分講義 - ルベーグ積分と面積0の不思議な図形たち- ,日本評論社,2003. | ||||||||
| [2] 新井仁之,実解析 掛谷問題とコロナ問題 - 日本発の二つの問題 -,数理科学 2000年12月号 (『数学の未解決問題』,サイエンス社,pp.100-110に再収録) | ||||||||
| [3] 新井仁之,掛谷問題のはじまり,数学セミナー 2002年8月号,pp.12-15. | ||||||||
| 原稿を公開中. | ||||||||
| ([3] には,掛谷宗一の直筆ノートに基づいて,掛谷宗一がどのような経緯から掛谷問題を思いついたのかを記してあります.掛谷の直筆ノートの写真がこちらにありますので,ご覧ください.) | ||||||||
| WEB版現代数学入門講座 第二回「リーマン関数とウェーブレット」はこちら。 | ||||||||
|
|
||||||||
| 著者のサイト | ||||||||
| 新井仁之のホームページ | ||||||||
|
|
||||||||
| 本ページに記載の文章、画像、動画の一部あるいは全部の無断転載、複写、複製することを禁じます。 | ||||||||
| --------- | ||||||||