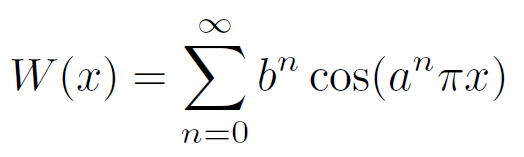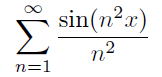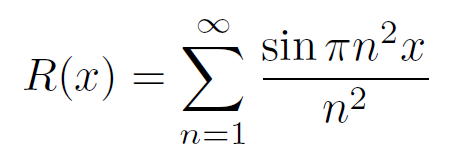| WEB版 現代数学入門講座 Vol. 2 (2016年11月5日) |
リーマン関数 |
ウェーブレット |
|
| |
|
|
| |
|
|
| |
|
|
| |
リーマン関数とウェーブレット |
|
|
|
|
Ver. 1.0 |
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
新井仁之(東京大学) |
|
| |
|
|
|
|
|
(2018~ 早稲田大学) |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
§1. リーマン関数の歴史 |
|
| |
みなさんは連続だけど、どの点でも微分不可能な関数を想像できますか? |
|
| |
このような関数が初めて世に出たのは 1872年、ドイツの数学者カール・ワイエルシュトラスにより考案されました。その関数は、 |
|
| |
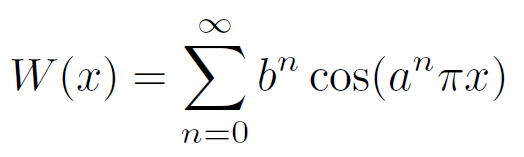 |
|
| |
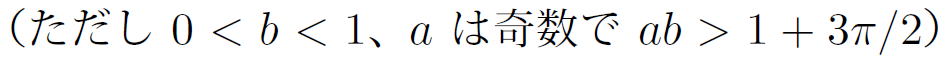 というものです。右辺の各項は無限回微分可能な関数ですが、その無限和をとると連続性は保たれるものの、微分可能性が至るところ崩れてしまうという驚くべき現象が起っているのです。 というものです。右辺の各項は無限回微分可能な関数ですが、その無限和をとると連続性は保たれるものの、微分可能性が至るところ崩れてしまうという驚くべき現象が起っているのです。 |
|
| |
ところで、ワイエルシュトラスはこの関数を独自に突然思いついたのではなく、その元ネタがあったことをご存じでしょうか? |
|
| |
ワイエルシュトラスの1872年の原論文[W]をひもとくと、次のような記述があります。 |
|
| |
|
|
|
|
|
|
|
|
| |
|
ごく最近に至るまで,実1変数の1価連続関数はいつでも 1 次導関数をもち,その値が不確定か無限大に発散するのは孤立したところでのみ起こり得ると一般的には信じられていた。私の知る限り、ガウス、コーシー、ディリクレといった自分たちの学問には至る所厳しい批判の目をむけることを常としていた数学者の著述の中にでさえ、彼らが反対の意見を持っていたことを疑問の余地なく読み取ることのできる言明は見つかっていない。リーマンの講義の聴講者数人から聞いたことだが、(1861年かあるいは多分それより以前に)初めてリーマンが、そのような思い込みはするべきではなく、たとえば無限級数
|
|
|
| |
|
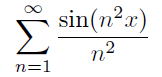 |
|
|
| |
|
で表される関数によってそれが正しくないことがわかると明言したのである。([W]より拙訳) |
|
|
| |
|
|
|
|
|
|
|
|
| |
しかし、ワイエルシュトラスはこの関数が任意の開区間の中に微分不可能な点を含むことを証明できませんでした。そこでワイエルシュトラスが思いついたのが
W(x) なのです。そして、彼は W(x) が連続であるにもかかわらず、何と至る所微分不可能であることを証明したのです。 |
|
| |
|
|
|
|
|
|
|
|
| |
では、もともとのリーマンによる関数の微分可能性はどのようになっているでしょう。ワイエルシュトラスですら手に負えなかった代物です。そう簡単にはいきそうにありません。 |
|
| |
この問題に最初に成果をあげたのはイギリスの数学者 G. H. ハーディです。インドの天才数学者ラマヌジャンを発見したことでも有名です。以下では記述を簡単にするためにリーマンの関数の変数にπをかけて、次のものを考えることにしましょう。 |
|
| |
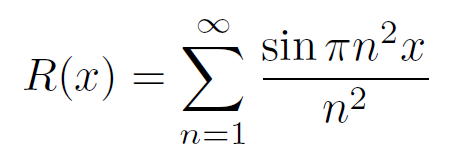 |
|
| |
ハーディはこの関数が、無理点で微分不可能であることを証明しました。どのような開区間の中にも無限個の無理点が入っているので、これによりリーマンの主張が証明されたことになります。またハーディはあるタイプの有理点でも微分不可能であることを示しました。1916年のことです。ワイエルシュトラスの論文から44年が経過していました。 |
|
| |
しかしながら、まだ問題が残されていました。それは一般に有理点での関数の微分不可能性(あるいは微分可能性)がどうなっているかということがわかっていませんでした。これが解決されたのはさらに55年たった
1971年です。J. ガーバー(Gerver)という人が (2A+1)/(2B+1) (ただし A と B は整数)という点で微分可能であること、そしてそれ以外の有理点では微分不可能であることを証明しました。 |
|
| |
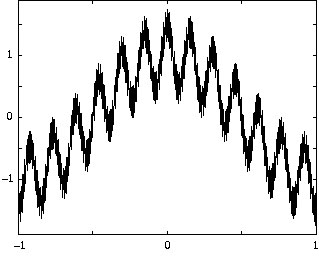
ここでリーマン関数とワイエルシュトラス関数のグラフを見ておきましょう。 |
|
| |
|
|
|
|
|
|
|
|
 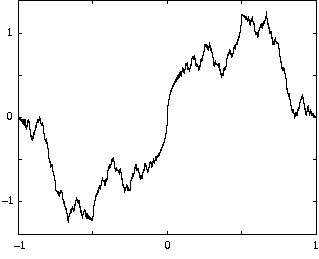 |
| |
|
図1 左:ワイエルシュトラス関数、右:リーマン関数 |
|
|
| |
|
|
|
|
|
|
|
|
| |
このグラフからもわかるように、ワイエルシュトラス関数はどこも同じようなギザギザなグラフですが、リーマン関数はかなり多様なタイプのギザギザがあるように見えます。 |
|
| |
|
|
|
|
|
|
|
|
| |
§2. 各点での滑らかさ |
|
| |
|
|
|
|
|
|
|
|
| |
滑らかさを測る一つの尺度にリプシッツ連続性(あるいはヘルダー連続性ともいう)があります。その定義をしておきましょう。 |
|
| |
|
|
|
|
|
|
|
|
 |
| |
|
|
|
|
|
|
|
|
| |
簡単な計算で、ワイエルシュトラス関数は -log(b)/log(a)-リプシッツ連続であることがわかります。仮定から、0 < -log(b)/log(a)
< 1 となっています。 |
|
| |
一方、リーマン関数の場合は、上記の微分可能な点以外では 3/4-リプシッツ連続ではない(すなわちそれ以下の滑らかさしかない)ことが知られています(ハーディ&リトルウッド;[J])。また、微分可能な点では
3/2-リプシッツ連続であることが示されています([J], [M])。 |
|
| |
|
|
|
|
|
|
|
|
| |
§3. 連続ウェーブレット変換 |
|
| |
|
|
|
|
|
|
|
|
| |
1980年代半ば、数学に新たな道具が加わりました。ウェーブレット変換です。ウェーブレット変換は画像処理、あるいは一般に信号処理の分野に大きな進展をもたらしました。これについては別の機会に講義をすることにします。ウェーブレット変換は、これまでフーリエ変換ではとらえられなかった各点でのリプシッツ連続性をとらえることができました([J],
[M], [JM], [HT])。ウェーブレット変換には連続ウェーブレット変換と離散ウェーブレット変換がありますが、ここでは連続ウェーブレット変換を扱うことにします。 |
|
| |
連続ウェーブレット変換についてはたとえば [A] を参照して下さい。(本講義の2として、この辺のことを詳しく解説する予定です。) |
|
| |
|
|
|
|
|
|
|
|
| |
§4. カスプ特異点と振動特異点 |
|
| |
|
|
|
|
|
|
|
|
| |
Y. メイエは連続ウェーブレット変換を用いて関数の二つのタイプの特異点の概念を導入しました。一つがカスプ特異点、もう一つが振動特異点です。この定義を述べるために二つの関数空間を導入しておきます。一つは
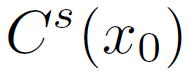 で、これは点 で、これは点 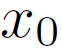 で s-次リプシッツ連続な関数の全体です。もう一つは次のものです。 で s-次リプシッツ連続な関数の全体です。もう一つは次のものです。 |
|
| |
|
|
|
|
|
|
|
|
 |
| |
|
|
|
|
|
|
|
|
| |
この二つの関数空間を用いて、各点ヘルダー指数 |
|
| |
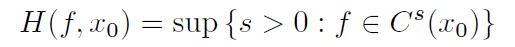 |
|
| |
と弱スケール指数 |
|
| |
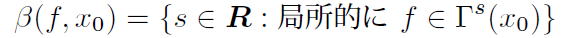 |
|
| |
です。 |
|
| |
そしてこの二つの指数がともに有限で一致す場合をカスプ特異点、また各点ヘルダー指数が弱スケール指数より真に小さい場合(弱スケール指数は∞でもよい)、振動特異点といいます。 |
|
| |
たとえばワイエルシュトラス関数はすべての点がカスプ特異点になっています([HW])。 |
|
| |
|
|
| |
§5. リーマン関数のカスプ特異点と振動特異点の可視化 |
|
| |
|
|
| |
メイエ [M] に依れば、リーマン関数 R(x) はカスプ特異点と振動特異点が混在し、たとえば 0 がカスプ特異点、1 が振動特異点になっていて、このことはシミュレーションによって可視化できると書かれています。 |
|
| |
このことを実際に確かめてみましょう。以下の計算で使ったのは MATLAB で、ウェーブレットとしてはドブシーのウェーブレット、db4 です。 |
|
| |
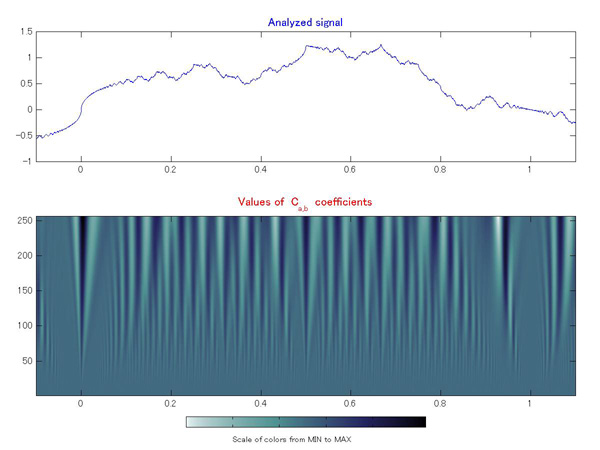
まずリーマン関数の連続ウェーブレット変換のグラフ(スケログラム)を計算してみます。結果は次のものです。 |
|
| |
|
|
|
|
|
|
|
|
 |
| |
|
図2. 上図:リーマン関数(ただし座標軸を見やすいようにスケーリングしてある)。下図:その連続ウェーブレット変換の強度グラフ。 |
|
|
| |
|
|
|
|
|
|
|
|
| |
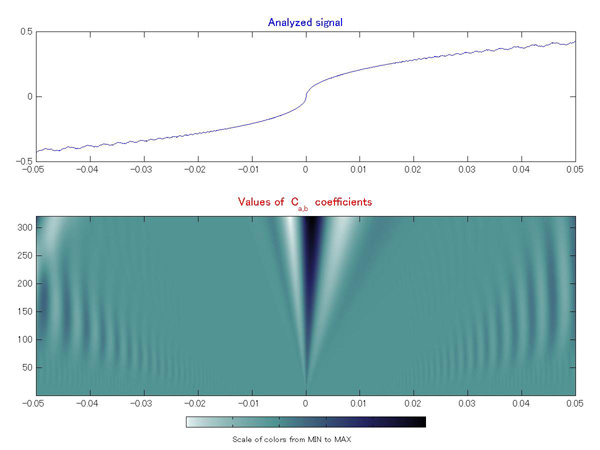
次にカスプ特異点である点 0 の部分を抜き出してみます。 |
|
| |
|
|
|
|
|
|
|
|
 |
| |
|
図3. リーマン関数のカスプ特異点(上)と連続ウェーブレット変換したもの(下)。 |
|
|
| |
|
|
|
|
|
|
|
|
| |
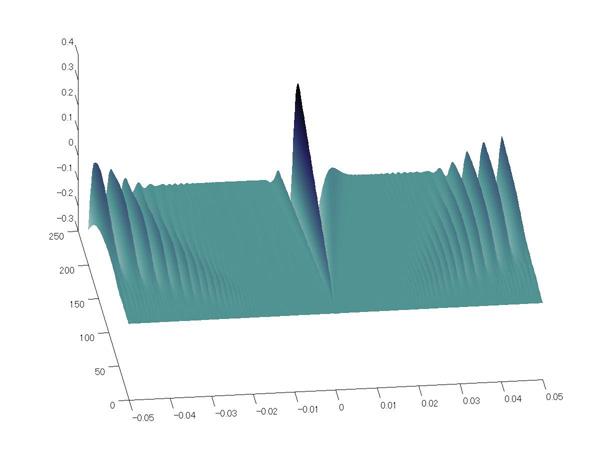
見やすいように 3D 表示します。 |
|
| |
|
|
|
|
|
|
|
|
 |
| |
図4. カスプ特異点(図3下)の 3D 表示。 |
|
| |
|
|
|
|
|
|
|
|
| |
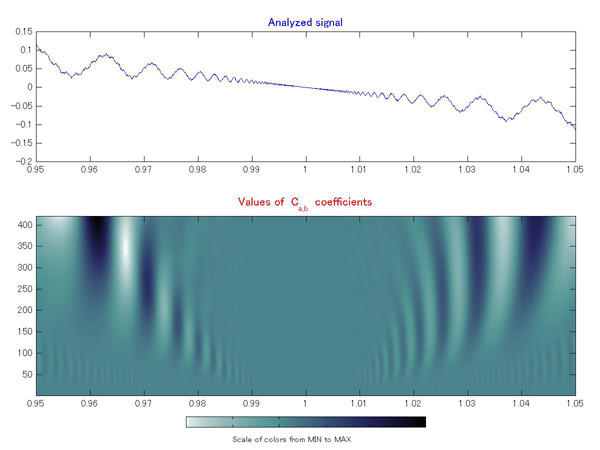
次に振動特異点である点 1 の部分をぬきだしてみましょう。 |
|
| |
|
|
|
|
|
|
|
|
 |
| |
図5. リーマン関数の振動特異点(上)と連続ウェーブレット変換したもの(下)。 |
|
| |
|
|
|
|
|
|
|
|
| |
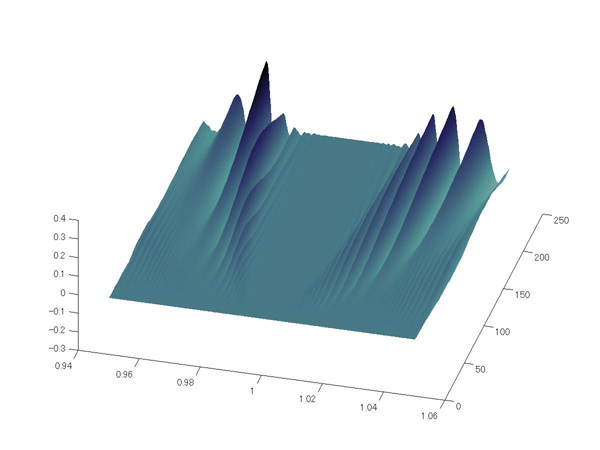
これも 3D 表示しておきましょう。 |
|
| |
|
|
|
|
|
|
|
|
 |
| |
図6. 振動特異点(図5下)の 3D 表示。 |
|
| |
|
|
|
|
|
|
|
|
| |
§6. まとめと次回講義予告 |
|
| |
|
|
|
|
|
|
|
|
| |
今回の講義ではリーマン関数の歴史と、各点での滑らかさ、カスプ特異点と振動特異点について述べました。さらに特異点の可視化も行ってみました。 |
|
| |
次回以降の何れかの回では、さらにリーマン関数の解析、それからカスプ特異点と振動特異点について掘り下げ、最近の話題に結びつけた話をする予定です。 |
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
*) 本稿の計算及び図版作成には MATLAB を使用しました。 |
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
参考文献 |
|
| |
[W] K. Weierstrass, Uber continuirliche Functionen eines reelen Arguments,
die fur keinen Werth des letzteren einen bestimmten Differentialquotienten
besitzen, (1872), Weierstrass Math. Werke II, 71--74. |
|
| |
[H] G. H. Hardy, Weierstrass's non-differentiable function, Trans. Amer.
Math. Soc. 17 (1916), 301--325. |
|
| |
[G1] J. Gerver, The differentiability of the Riemann function at certain
rational multiples of π, Amer. J. Math. 92 (1970), 35--55. |
|
| |
[G2] J. Gerver, More on the differentiability of the Riemann function,
ibid 93 (1971), 33-41. |
|
| |
[HT] M. Holschneider and P. Tchamitchian, Pointwise analysis of Riemann's
"non differentiable" function, Invent. Math. 105 (1991), 157-176. |
|
| |
[J] S. Jaffard, The spectrum of singularities of Riemann's function, Revista
Mat. Iberoamericana 12 (1996), 441-460. |
|
| |
[JM] S. Jaffard and Y. Meyer, Wavelet methods for pointwise regurality
and local oscillations of functions, Memoirs of Amer. Math. Soc., vol.
123, 1996. |
|
| |
[M] Y. Meyer, Wavelets, Vibrations and Scalings, CRM Monograph Ser. vol.
9, Amer. Math. Soc., 1998. |
|
| |
[HW] H. Watanabe, On the scaling exponents of Takagi, L\'evy and Weierstrass
functions, Hokkaido Math. J., 30 (1) (2001), 589-604. |
|
| |
[A] 新井仁之、ウェーブレット、共立出版、2010. |
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
WEB版現代数学入門講座 第一回「掛谷問題ショートコース」はこちら。 |
|
| |
|
|
|
|
|
|
|
|
|
| 錯視の科学館の外部からアクセスしている方は,次をクリックしてください.錯視の科学館入口です. |
| |
|
|
 |
|
|
|
| |
|
|
|
|
|
|
|
|
| このページの著作権は新井仁之にあります.本ページに記載の内容・画像の一部あるいは全部の無断転載を禁じます. |
| |