錯視	産業	技術	数学	数理科学	視覚科学	知覚心理学	画像処理	3/4ページ
(独)科学技術振興機構(JST)  戦略的創造研究推進事業　個人型研究　さきがけ JST 数学領域 数学と諸分野の協働によるブレークスルーの探索
						錯視，視覚の数理モデリング，そして錯視から拡がる数理科学と科学技術の融合的研究
数理視覚科学とは何か　−　新しい学術分野の提唱
		東京大学大学院数理科学研究科 教授
			新井 仁之
	前ページで述べた視覚の数理モデリングの研究は，視覚のほか，錯視の研究，純粋数学の研究などいくつかの分野とも関連してきます．まず錯視についてから述べることにしましょう．
錯視の研究にどのように役に立つのか？
	視覚の数理モデルの研究は，錯視の研究そのものにもたいへん新しい結果をもたらしています．このことについて研究結果の一つを紹介したいと思います．
			左の図形で，水平方向に灰色の線が何本かあります．これらは平行なのですが，傾いて見えるという錯視です．この錯視はカフェウォール錯視 (cafe wall illusion) と呼ばれています．
	数学を用いると，この錯視図形から錯視成分を特定することができます，そしてさらに錯視成分を抜き出して，錯視を除去することができます．下の図をご覧ください．左がカフェウォール錯視の錯視成分，右が錯視成分を抜き出して錯視を除去した図形です，錯視を除去できました！(これは H. Arai & S. Arai, VISION, 2005に発表した結果です)
							錯視が消えた
		左：錯視成分，中央：錯視を除去
	このほか，Gregory と Heard により見いだされた次のような現象を，数学的に明らかにしました．
	カフェウォール錯視では，平行な線は濃い灰色のボックスとうすい灰色のボックスの間の輝度を持っています．しかし水平線の色を，黒いブロックよりもより濃い黒にしたり，水平線の幅を広げると錯視量が激減します．特に下の右図では逆錯視も起こっていることが指摘されています．なぜこのようなことが起こるのでしょうか？
	私の考案した数理モデルを使って，こういった現象も数学を用いて説明できます．
	詳しい説明はかなり専門的になってしまうので，次の論文あるいは次ページの解説文をご覧ください．
	H. Arai, A nonlinear model of visual information processing based on discrete maximal overlap wavelets, Interdisciplinary Information Sciences, 11 (2005), 177-190.
	このほかにも．ヘルマン格子錯視，シェブルール錯視，マッハの帯の錯視，明暗の対比錯視をはじめ，ある種の錯視を統一的な方法でコンピュータに発生させることに成功しました．また次頁の色つきマッハリングもこれらと同じ手法でシミュレーションできました．
	さきがけでは，さらに幾何学的錯視，色に関する錯視，数学的方法による新しいタイプの錯視の作成などについて研究を進め，視覚の研究を行っています．
数学で錯視を作る!?
	じつは，数学と神経科学的な考察をすることにより，どのような画像でもある種の錯視画像に変えることに成功しました．この計算アルゴリズムは現在を特許を出願中です(新井・新井，JST, 2010)．
	ともかくこの計算アルゴリズム(浮遊錯視生成アルゴリズム)を使って作成した錯視画像の一つをご覧いただきましょう． 「リースの浮遊錯視」です．
		錯視画像の見方：中央の丸印を見ながら，顔を画像に近づけたり，画像から遠ざけたりしてください．すると，リースの輪が円上を浮遊しているように見えます．また首を傾げると，リースの輪が伸縮するようにも見えます．
Copyright Hitoshi Arai and Shinobu Arai, Dec., 2011.
	これまで，静止画なのに動いて見える錯視画像は，特殊なパターンを見出して作成されてきました．新井・新井の発明した浮遊錯視生成アルゴリズムは，錯視に詳しくない人でも自分の好きな画像から新しい浮遊錯視を作成できるのです．数学は魔法のようですね．
数学そのものにも寄与できるか？
	視覚の数理モデルに必要な 新しい数学 も開発しています．たとえば
			かざぐるまフレームレット
	を新しく発見しました．フレームレットという枠組みはウェーブレットという数学をより進化させたもので，2003年頃から応用数学者たちによって研究されています．私たちのかざぐるまフレームレットは，視覚の数理モデルに適した新しいフレームレットの一つです．
	新井・新井(2009)による定常単純かざぐるまフレームレット．
	方位選択性は自由に増やすことができる．数学的にはODOGより優れた点が多々ある．
	このほかにも幾何的フィルタリングなど新しい方法を考案しました (2010)．視覚の研究をさらに進めるためには，新しい数学的な道具もいろいろ開発していく必要があります．こういったことは，おそらく数学そのものの発展にも寄与するはずです．
科学技術の諸分野，産業への応用があるのか？
	まず述べておきたいことは，このような研究は，私たちがどのようなメカニズムでものを見ているのかを解明するのに役立ちます．つまり視覚科学，知覚心理学などとも深く関連しています．
	それ以外に役立つこととしては，コンピュータ・ビジョンをはじめ，画像処理に関連する産業，医療に応用があると考えています．ゆくゆくはロボットの視覚の研究にもつながっていくでしょう．
	このほかには，視覚の数理モデルのために開発している新しい数学である「かざぐるまフレームレット」が，おそらく画像工学に役立つと考えています．また，色に関する錯視の研究は，色彩に関連するさまざまな産業の分野にも影響を与えるはずです．
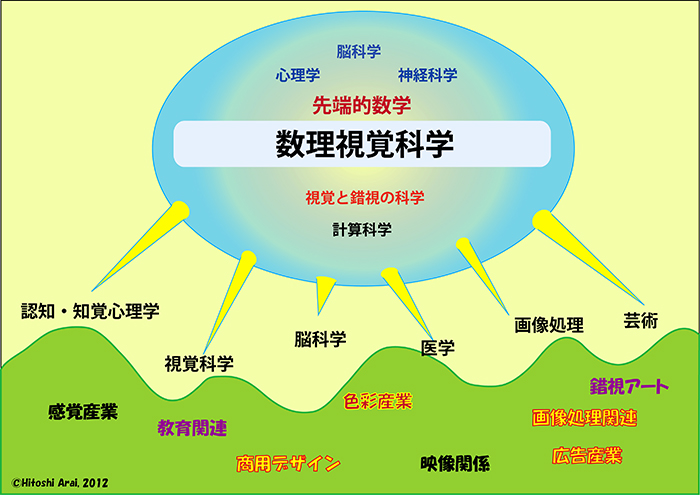
		数理視覚科学と科学、産業との関係図
			新しい創成型産業数学
	従来の産業数学は、既存の産業をアシストするというタイプのものがほとんどでした．それに対して，数理視覚科学では知覚・感覚・認識に関する新しい産業を生み出すことも目標の一つにしてます．その意味では，筆者のネーミングですが，創成型産業数学といえるものです． 　もちろん数理視覚科学は既存の産業への応用の可能性も含んでいます．たとえば，視覚に関連して，色彩産業，医療技術，画像・メディア産業，デザイン産業，広告産業などです．
			他のページを読む
	本ホームページの全部あるいは一部の無断転載・複製を禁止します．