Tweet
			掛谷問題のはじまり
			新井仁之
	拙著『掛谷問題のはじまり』は、「数学セミナー」（2002年8月号）に掲載されたが、この雑誌が刊行されてからかなりの歳月が経ち、入手が極めて困難な状況である。 そのため、もはや一般の方がこの原稿を読むことは、大学の図書館にでも行かない限りほぼ不可能なものとなっている。しかし、『掛谷問題のはじまり』は、筆者の調査により初めて明らかになったことであるが、掛谷宗一がどのようにして掛谷問題を見いだしたのか、その経緯を克明に記してあり、歴史的価値のあるものと考えている。そこで、このサイトでは、掛谷問題の起源をできるだけ多くの方に知って頂きたいと考え、筆者の原稿を載せた。
	はじめに、筆者がどのようにして掛谷問題の起源を「発見」したのかを簡単に述べ、『掛谷問題のはじまり』を執筆するに至った経緯を記しておきたい。
	『掛谷問題のはじまり』を書いた経緯
	1999年に私は東北大学から東京大学に移動し，東大の数理科学研究科の図書室を利用するようになった．そこで初めて図書室に掛谷宗一直筆の研究ノートの複写が保管されていることを知った．早速その複写を見ると，そこには掛谷が主に東北大学在職中に研究したことが日記のように事細かに記されていた．もしかすると掛谷問題についても何か書かれているのではないだろうか．そう思って特に大正初期の部分を重点的に調べることにした．調べるうちに大正5年11月23日から数日間にわたって掛谷問題に関する記述があることを見出した．そこには掛谷問題に関する数学的な記述のほか，掛谷問題誕生の真相が一部始終書かれていた．それには有名なエピソードである武士が厠で槍を回転させる件は書かれておらず，実に意外な記述があった．東北帝国大学教授藤原松三郎，窪田忠彦のほか，同総長北条時敬も重要な役割を果たしていた．
	このことはおそらく衝撃的なことである（少なくとも筆者にとってはそうであった）。そこで、できるだけ詳しく掛谷問題のはじまりを直筆ノートの写真入りで紹介したいと思い、『掛谷問題のはじまり』を執筆した。
	ところで東大数理にあるものは複写だったので，原本がどこかにあるのか図書室の人に調べてもらった．それによりノートは統計数理研究所に所蔵されていることがわかった．そこで統計数理研究所を訪れ，掛谷ノートの実物を見ることができた．下記の写真はそのとき研究所図書室の許可を得て撮影したものである．
掲載誌：「数学セミナー」2002年8月号 pp.12-15
掛谷問題のはじまり -- 掛谷宗一の直筆ノートより --
					新井仁之
１
数学者はどのように問題を見つけ，そしてそれをどのように研究していくのだろうか？数学の場合，印刷された論文からそれをうかがい知ることはほとんどできない．もし数学者が自分の研究の舞台裏を一部始終記録しており，しかもそれがどこかに保存されていたならば，後世の者はそこから思考の跡を探ることもできる．しかしそのようなものが残されているのは極めてまれなことである．ところが幸運にも本特集の主人公，掛谷宗一は研究の過程をまるで日記のようにノートに書き留め，しかもその一部が統計数理研究所の図書室に所蔵されているのである．保存されいるのはA5判の大学ノート27冊など，主として大正時代に書かれたものである．時期的にはちょうど幾何学における掛谷問題
	長さ l の線分を一回転することのできる凸の図形で，面積最小のものは何か？
に相当するものがが論文として印刷・発表された年，大正6年を含んでいる．
ここでは掛谷直筆の研究ノートに基づいて，掛谷問題がどのようにして生まれたのか，当時の様子を再現しながらみていくことにしよう．
掛谷宗一研究ノート（統計数理研究所所蔵）研究所の許可を得て筆者撮影
				２
掛谷問題に関する記述は大正5年11月23日から始まる．当時掛谷は東北大学の助教授であった．ノートによれば，ことの発端は「食堂」で起こった．食堂というのは，おそらく東北大学片平キャンパス内の大学の食堂のことであろう．そこには数人の数学関係者が席をともにしていたものと思われる．その席で当時34才になる藤原松三郎教授が正三角形の内転形の模型を一同に紹介していた．藤原は今日では大著「微分積分學」，「代数學」(内田老鶴圃)の著者としても有名だが，林鶴一とともに創設時の東北大学数学教室を支えた人物である．藤原の見せた模型がどのようなものであったのか残念ながらノートからは不明であるが，参考までに藤原-掛谷の内転形と呼ばれているものをあげておこう (図1参照)．
図1 動画はこちら
さて藤原が紹介していた模型を見ている人々の中に北条時敬という人物がいた．北条は当時の東北大学総長で，かつて東京大学で数学を学んだこともり，数学には明るかった．北条が何気なく訊ねた．
『この内転形が一回転するのに必要な最小の図形はこの正三角形ですか？』
	－以下『　』内は掛谷のノートに基づく記述である．ただし読みやすくするため筆者の独断で現代文・現代かなづかいに直した．そのため原文の格調は失われてしまった．原文は掛谷ノートを参照してほしい．原文の一部は[4] にも記してある．
この瞬間，掛谷の鋭い数学的な嗅覚が働いた．学者にとって種々雑多な情報の中から重要なものを嗅ぎ分ける能力は必要不可欠なものであるが，掛谷の場合，その力は人一倍長けていた．それは彼のいくつかの仕事を眺め，その問題のとらえ方を見ればわかる．掛谷はその瞬間の様子を次のようにノートに記している．
『(北条総長の)言った一言を聞き，私は非常に面白いと感じた．そしてここにおいて直ちに次のような一般的な問題を創った．与えられた平面図形 A が平面上を一回転するのに要する最も狭い場所を求めよ．』 (写真1参照)
	ノート1
彼は早速この問題の考究をはじめた．そしてこれまでの習慣どおり，研究の一部始終はノートに克明に書きとめられた．
ノートは，
『総長問題』
という言葉で始まっている．もちろん北条総長が発した質問を意識してのことである．まずはじめに問題を考えるに至ったいきさつを一通り記録した後，一頁ほどかけて最初の考察の過程を書いた．この部分から掛谷はどうやら三角関数を使って解こうとしたらしいことがわかる．しかし，そう簡単には答えに到達できないと感じたのか，あるいは確かな手ごたえを感じたために整理しなおして考え始めようとしたのか，彼は今まで記したところすべてにわたって大きな斜線を引いた．そして次のページにすべてを最初から書き改めはじめたのである(写真1，2参照)．問題を思いついたいきさつからである．この時点においてすでに掛谷は，考えている問題が総長の何気なく言い出した質問に端を発する軽いものではなく，じつは数学の奥深いところを突いた重要なものであることを察知していたものと思われる．標題を「総長問題」から数学的普遍性をもつ
『Smallest domain of revolution』
と改めた．この部分のノートをじかに見ると，彼が襟を正して問題に向かいなおしている姿が彷彿としてくる．
		ノート2
しかし残念ながらまたしても問題を解くには至らなかった．掛谷はそのときの思考の足跡を4ページほどかけて記したあと，
『この論は失敗に終った．次のページより改めて論ずる』
と書いている．11月23日のことである．
次に再び標題を
『Smallest domai of revolution, I，5,11,23-28』
と書き改め(写真3)，新たなアタックを始める．今度は11月23日から28日と日付を書いていることから，6日間にわたる攻略が続いたものと思われる．掛谷はまず次のように問題の単純化を計る．
		ノート3
『問題を簡単にするために(回転する図形) X は一つの卵形線とし，一回転に要する図形も卵形であるとして観察をする.』
そして例として
『X が直線の一部であるとき』
を考えた．幾何学における「掛谷問題」の誕生の瞬間である．掛谷はこの問題に対する答えとして，写真5 のような図形を描いた．しかし特に詳細な証明は見当たらない．掛谷にとってこれは具体例の一つに過ぎなかったのであろう．すぐに一般の場合へと考察を広げていった．
ところが，X が直線の一部の場合に掛谷が得た答えは誤りであった．日にちははっきりしていないが，おそらく11月28日に近い日，掛谷の同僚の藤原松三郎と窪田忠彦（当時東北大学助教授）から次のような指摘を受ける．
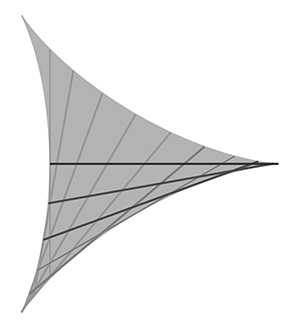
『只今窪田，藤原両君よりのご注意によりノートのp.82第一図(ノート4) の example は誤りであることが発見された．すなわち高さ l の正三角形の方が一回転できる面積の小さい図形であることが注意された．なお窪田君はさらにこれより小さいが凸ではない図を示された(図2参照)．そのため私はここに改めてこの例題を研究する．すなわち直線 l が一回転できる面積最小の凸図形を求めよ．』
		ノート4
			図2動画はこちら
掛谷の頭の中では，問題の難しさがはっきりと認識されたに違いない．彼はまず自分がなぜ間違えたのかを検討した．そしてさらに研究を進めていった．
結論を先に言ってしまえば掛谷の努力にもかかわらず，残念ながら彼は最終的な解答に達することはできなかった．問題を制したのは，J. Pa'l という人だった．5年後の1921 年 (大正10年)，Pa'l は藤原の指摘した高さ l の正三角形が掛谷の問題の正しい答えであることを証明したのである．さらに 1928 年 A. Besicovitch が凸図形という制限を落とした場合，窪田の考えた図形が面積最小のものではなく，じつはどのように小さな正数 ε を与えようとも，長さ l の線分が一回転できる図形で面積が ε より小さいものを作れるということを証明した．
時間は飛び，それから50年後．掛谷の仕事が実解析学で再び注目を浴びることになる．1971年に C. Fefferman が掛谷問題の発想を援用して，多変数フーリエ解析の懸案の問題を誰もが予想しなかった形で解いたのである．この衝撃はさらに実解析学上の重要なある未解決問題へと発展していった．その未解決問題は現在「掛谷問題」あるいは「掛谷予想」と呼ばれている．これらについては，本特集の後半で詳しく紹介したい．
				３
最後に，掛谷宗一のプロフィールを簡単に紹介しておこう．掛谷は明治19年(1886年)に広島県深安郡坪生村に生まれた．明治39年に第三高等学校を卒業，東京帝国大学(現東京大学)に進学し，明治42年には同数学科を卒業した．在学中から掛谷の数学的才能は注目を浴び，2年次，3年次では特待生，また3年進級時にはDavid Murray記念数学賞を受賞している([3])．卒業後，明治44年に第一高等学校の教授，明治45年に東北大学理科大学(現東北大学理学部)助教授となり，その後東京高等師範学校教授などを経て，昭和10年からは東京帝国大学で教授として教鞭をとった．さらに昭和19年から21年まで東京帝国大学理学部長，また昭和19年より昭和22年に没するまで統計数理研究所の初代所長を勤めた．
掛谷の数学的な業績は多岐にわたっている．研究対象は本特集で紹介されている幾何学的な掛谷問題をはじめ，卵形線の研究，代数方程式，連立積分方程式，解析関数，フーリエ級数など幾何学，代数学，複素解析，実解析の分野を縦横無尽に駆け回るものであった．特に連立積分方程式の研究では帝国学士院恩賜賞を受賞している．掛谷の研究は幅広さとともに深みをもち，しかも「人の仕事の真似ごとでなく，自分で新しい問題をつかみ，自分で考える」(河田龍夫『私の先生方の思い出』，[3] に収録)という独創性に富むものであった．
その掛谷の数学的な成長にとって，明治45年から大正9年までの東北大学に在職した時期は極めて重要なものであったといえよう．実際，掛谷問題をはじめ帝国学士院恩賜賞の対象となった研究を含め，多くの重要な仕事がこの時期に行われている．現在残されているノートもこの時期のものである．
なおノートはその他にもたくさんあったようであるが，それらは戦災で焼けてしまったらしい．失われたノートの中には，未発表の研究成果も含まれており，たとえばvan Dantzigよりも以前に線形計画法のsimplex methodを考えていたことが記されていたという(河田前掲記事)．何とも残念なことである．
参考文献 [1] 掛谷宗一，研究ノート, 統計数理研究所所蔵. [2] S. Kakeya, Some problems on maxima and minima regarding ovals, The Science Reoports of the Tohoku Imperial University, Ser.1, Mathematics,Physics, Chemistry, 6 (1917), 71--88. [3] 佐々木重夫，東北大学数学教室の歴史，東北大学数学教室同総会発行, 1984. [4] 新井仁之，掛谷問題とコロナ問題 - 日本発の二つの問題 -，数理科学, 2000 (12), 56--65. [5] H. Arai, The birth of Kakeya's problem -- from his autograph note books --, in preparation for publication.
						（あらいひとし）
	注：図１, 図２は2002年の原稿を元に描画しなおしてあります。
掛谷問題の概説は「掛谷問題ショートコース」をごらんください．
図1，図2の動画へのリンクは 2022/3/15に追加したものです．
このページの著作権は新井仁之にあります．本ページに記載の内容・画像の一部あるいは全部の無断転載を禁じます．