キャッシュをご覧になっている場合があります．更新して最新情報をご覧ください   
  デジタル時代の新しい大学レベルの学びの場   
数理科学デジタルオープンレクチャーズ
  Digital Open Lectures in Mathematical Sciences  
  数学 数理科学 オンライン公開講座  
                 
                 
      企画・制作　新井仁之
              プロフィール 
                 
                 
  世界中のさまざまな大学において授業のオンライン公開配信、すなわちオープンコースウェア(Opencourseware, OCW) が行われています｡ そのような中で、数学・数理科学専用の OCW をぜひ作りたいと思い、誰もが自由に学べる  
     
  数理科学デジタルオープンレクチャーズ   
  Cyber Akademeia: Digital Open Lectures in Mathematical Sciences   
     
  を始めました。  
  　ただし数理科学デジタルオープンレクチャーズは，通常の OCW と違い，大学の授業を配信するのではなく，オリジナルコンテンツを制作し配信することをポリシーとしています。というのは大学のカリキュラムの一環として学ぶオンライン授業が、自由な立場で自習する場合、内容によっては必ずしも学び易いとは限らないからです。講義のストーリー展開や説明に工夫が必要です。数理科学オープンレクチャーズでは、分かり易く、質の高いオンライン公開専用のオリジナル講義を作成しています。  
     
  　なお、本プロジェクトは企画立案から動画作成・発信まですべての作業を個人で行っています。そのため，残念ながら不定期配信になりがちです。しかし質の高い，他では視られないような  
  大学/大学院レベルの一般向け講義、専門的な講演  
  などのオリジナル・コンテンツを充実させていきます。  
  　線形代数と深層学習についてはプログラミング教材もあります。  
     
   オンライン授業の優れた点は  
  いつでも、どこでも、誰でも  
  視聴できることです。対面授業にはないこの利点を活かして、数理科学デジタルオープンレクチャーズでは，どなたでも受けることのできる、さまざまなコースを用意してあります（更に拡充中です）。もちろん、受講料無料、事前手続き無しのオンラインの公開講座です。  
  　近年、教育のデジタル化が急速に進んでおりますが、そのような中で、本プロジェクトがインターネットを利用した数学・数理科学の一般向け教育、STEM教育、STEAM教育、ギフテッド教育、あるいは大学教育のデジタル化、デジタルトランスフォーメーション（DX）促進にも繋がるものと考えています。  
                 
   
  *) なお配信には YouTube を使用していますが、収益化は行っていません。
                 
                 
                 
    コース    
                 
  更新中のコースは適宜コンテンツを増やしていく予定です。 また融合的なテーマの場合、コースの内容が別のコースとリンクすることもあります。       
  講師　新井仁之  
                 
  ↓タイトルをクリックすると動画（YouTube）が見られます。        
                 
ルベーグ積分と実解析コース　（更新中）         
  No.1 イメージがわかるルベーグ測度入門           
  No.2  イメージがわかるルベーグ積分入門       
  No.3  ルベーグ集合とは      
  No.4  実解析と確率論 - マルチンゲール，ブラウン運動，実解析    
  No.5  ダニエル積分とその使い方 - 確率論への応用   
  No.6 観てわかるLp 空間とノルム空間　Lp空間入門 No.1   
  No.7 観てわかるLp空間の完備性とスモールlp空間　Lp空間入門 No.2  
  No.8 微分同相写像によるルベーグ積分の変数変換公式
                 
フーリエ解析コース　（更新中）           
  No.1 フーリエ級数展開はコロンブスの卵的な発想だった　　
  No.2  動画で学ぶフーリエ級数の収束定理       
  No.3 超関数とフーリエ変換入門      
                 
ウェーブレット解析コース　　（更新中）           
  導入 フーリエキングダムとウェーブレット革命  
  No.1  窓付きフーリエ変換から連続ウェーブレット変換    
  No.2  ハール・ウェーブレットと多重解像度解析       
                 
応用線形代数コース　 （更新中）           
  No.1 特異値分解入門　- 基礎から画像処理への応用まで -  
  No.2  一般逆行列入門  
  No.3  正規直交基底と離散フーリエ変換の基礎      
  教材 プログラミングしながら学ぶ応用線形代数と深層学習   
                 
微分積分コース 　   （更新中）         
  No.1  14分でわかるエプシロン-デルタ論法入門 - その意味と使い方-    
  No.2 微積分の基礎を38分で一気に解説  
  No,3 手品のような定理 - ボルツァノ・ワイエルシュトラスの定理  
  No.4 連続だが至る所微分不可能なワイエルシュトラス関数       
  No.5 d次元ユークリッド空間の距離，開集合，閉集合 - 多変数関数の極値問題に向けて 
  No.6 多変数関数のテイラー展開徹底講義 No.1 - 多重指数で簡単表示
  No.7 多変数関数のテイラー展開徹底講義 No.2 - しっかり解説、定理と証明
  No.8 多変数関数のテイラー展開徹底講義 No.3 - 勾配ベクトルとヘッセ行列による表示
                 
関数解析コース 　（更新中）           
  No.1  ワイエルシュトラスの多項式近似定理の面白い発展       
                 
応用解析コース　 （更新中）          
  No.1 超関数論への誘い - 15分でわかる超関数の考え方    
  No.2 ヒルベルト変換入門 - ヒルベルト変換と解析信号 -  
  No.3 ソボレフ空間入門 -基礎から埋め込み定理とその応用まで（証明も解説）- 
  No.4 ディジタル信号処理の数学的基礎，サンプリング定理入門 - 解説と証明-
                 
画像処理入門コース 　（更新中）           
  No.1  画像と線形空間       
  No.2  離散コサイン基底  
                 
ディープラーニング入門コース　（更新中）        
  No.1  順伝播型ニューラルネット       
  No.2 誤差逆伝播法       
  教材 プログラミングしながら学ぶ応用線形代数と深層学習   
                 
錯視科学特別コース　　（更新中）            
  No.1  水彩錯視のパワポやグリーティングカードへの応用    
                 
                 
特別講義 1 掛谷予想            
  No.1  掛谷予想の前哨戦 - 掛谷予想が生まれる背景  
  No.2  ベシコヴィッチの定理とベシコヴィッチ・モンスター  
  No.3  掛谷予想とハウスドルフ次元  
  No.4  多変数フーリエ解析と掛谷予想      
                 
特別講義 2 フラクタル            
  No.1  イントロダクション：コッホの雪片曲線  
  No.2  様々な自己相似集合  
                 
オンライン談話会            
    ICT活用と協働した微分積分教育の内容の変革と実践について - 早稲田大学の微積分1A/2A で実践した大学教育のデジタル化とデジタルトランスフォーメーションへの展望。 (微積分1A/2AでWaseda e-Teaching Award を受賞したときの概要動画)   　
    解説文はこちら（早稲田大学のHPより）       
                 
                 
    コンテンツ紹介（配信順）    
                 
  第37回配信       
  手品のような定理 - ボルツァノ・ワイエルシュトラスの定理       
                 
  ボルツァノ・ワイエルシュトラスの定理    
           
  微積分や解析学で重要なボルツァノ・ワイエルシュトラスの定理とその区間収縮法による証明をていねいに解説します。これは次の手品のような定理です。
「好きな有界数列を考えてください。」
「その中から，必ず収束するような部分列を見つけてみましょう。」
 
 
                 
                 
                 
  第36回配信          
  ディジタル信号処理の基礎　シャノンのサンプリング定理       
                 
  シャノンのサンプリング定理    
  2023/06/14      
  ディジタル信号処理の基礎であるシャノン（-染谷ら）のサンプリング定理について解説し、また数学的に厳密な証明も講義します。CDのサンプリング周波数についても触れます。
 
 
                 
                 
                 
  第35回配信       
  微分同相写像によるルベーグ積分の変数変換公式       
                 
  微分同相写像による変数変換公式    
  2023/05/20      
  重要な定理であるにもかかわらず，その証明を読むのはしんどい定理の一つです。その証明を丁寧に解説します｡            
 
 
                 
                 
                 
  第34回配信       
  多変数関数のテイラー展開徹底講義 No.3 - 勾配ベクトルとヘッセ行列による表示       
                 
  gazou        勾配ベクトルとヘッセ行列による表示    
  2022/09/18      
  多変数関数のテイラーの定理徹底講義３部作のうちの No.3 です．テイラーの定理の勾配ベクトルとヘッセ行列による表示を解説します．この形はタイ変数関数の極値問題で使われます．知っていると便利な形です．            
 
 
                 
                 
  第33回配信    
  多変数関数のテイラー展開徹底講義 No.2 - しっかり解説、定理と証明       
                 
  gazou         しっかり解説、定理と証明    
  2022/09/18    
  多変数関数のテイラー展開徹底講義３部作のうちの No.2 です．多変数関数のテイラーの定理の証明をじっくりと解説してあります．
 
 
                 
                 
  第32回配信       
  多変数関数のテイラー展開徹底講義 No.1 - 多重指数で簡単表記       
                 
  gazou 多重指数で簡単表記    
  2022/09/18      
  多変数関数のテイラーの定理徹底講義３部作のうちの No.1 です．テイラーの定理をはじめ，偏微分方程式論などでひんぱんに用いられている多重指数を丁寧に解説し，テイラーの定理を多重指数の記法を使って述べました．証明は No.2 で行います．            
 
 
                 
                 
  第31回配信       
  ディープラーニングの基礎入門 No.2 - 誤差逆伝播法       
                 
  gazou 誤差逆伝播法    
  2022/7/25      
  ディープラーニングの基本的な事柄について，特に誤差逆伝播法に関する数学的な基礎事項を丁寧に解説しました．            
 
 
                 
                 
  第30回配信     
  ディープラーニングの基礎入門 No.1 - 順伝播型ニューラルネット   
                 
  gazou 順伝播型ニューラルネット    
  2022/7/25      
  ディープラーニングの基本的な事柄について，数学的な基礎事項を丁寧に解説しました．           
 
 
                 
                 
  第29回配信    
  d次元ユークリッド空間の距離，開集合，閉集合 - 多変数関数の極値問題に向けて     
                 
  gazsou 多変数関数の極値問題に向けて    
  2022/7/25       
  多変数関数の極値問題に向けての準備，d次元ユークリッド空間の基礎事項を解説しました．            
 
 
                 
                 
  第28回配信           
  微積分の基礎を38分で一気に解説      
                 
  gazou 微積分の基礎を38分で一気に解説    
  2022/5/28       
  連続性の公理からボルツァノ・ワイエルシュトラスの定理，中間値の定理，実数の完備性まで．微積分への序説．            
 
 
                 
                 
  第27回配信           
  14分でわかるエプシロン-デルタ論法入門 -その意味と使い方-       
                 
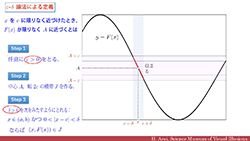  gazou 14分でわかるエプシロン-デルタ論法入門    
  2022/3/8    
  大学で学ぶ微分積分の最初の障壁とされるエプシロン-デルタ論法．その定義の意味とε-δ論法の使い方を，例題や応用例を交えながら，わかりやすく解説します。          
 
 
                 
                 
  第26回配信           
  ソボレフ空間入門 -基礎から埋め込み定理とその応用まで（証明も解説）-
                 
  gazou ソボレフ空間入門 - 基礎から・・・    
  2022/3/8      
  ユークリッド空間上のソボレフ空間の基礎から，ソボレフの埋め込み定理と簡単な楕円型偏微分方程式（ポアソン型方程式）への応用までを解説しました。
 
 
                 
                 
                 
  第25回配信           
  ヒルベルト変換入門 - ヒルベルト変換と解析信号 - Ver.2        
                 
  gazou ヒルベルト変換入門 - ヒルベルト変換と解析信号-    
  2022/3/6, 2022/3/7      
  複素解析，信号解析，微分方程式論などにしばしば現れるヒルベルト変換。この講義では，ヒルベルト変換を数学的厳密さを失わないように，信号解析，複素解析などとの関連を絡めながら解説しました。            
 
 
                 
                 
                 
  第24回配信           
  フーリエ級数展開はコロンブスの卵的な発想だった　フーリエ級数ことはじめ
                 
  gazou フーリエ級数展開はコロンブスの卵・・・    
  2021/12/31 　現在 update 準備中    
  フーリエがすべての関数がフーリエ級数展開できると考えるに至った経緯を分析してみます。フーリエ級数論への入門講義です。
 
 
                 
                 
                 
  第23回配信           
  ワイエルシュトラスの多項式近似定理の面白い発展  
                 
  ワイエルシュトラス多項式近似定理 ワイエルシュトラスの多項式近似定理の面白い発展    
  2021/11/14      
  ワイエルシュトラスの多項式近似定理って多変数でも成り立つの？複素変数にしたら？こういった疑問にお答えします。じつはワイエルシュトラスの多項式近似定理の一般化は大きな広がりをもっています。今回のレクチャーではその一部を解説します。           
 
 
                 
                 
                 
  第22回配信　談話会         
  ICT活用と協働した微分積分教育の内容の変革と実践について   
                 
  ICT ICT活用と協働した微分積分教育の内容の変革と実践について - 早稲田大学の微積分1A/2A で実践した大学教育のデジタル化とデジタルトランスフォーメーションへの展望。
  2021/10/18   
  微積分の教育内容を人工知能やビッグデータ等の数理時代のニーズに適うよう改革し、それにICTを協働させた話しです。大学教育のデジタル化、教育のデジタルトランスフォーメーション（DX）の事例であり、e-Lerning、e-Teaching 、教育内容改革の協働の例でもあります。     
 
 
                 
                 
                 
  第21回配信            
  フーリエ解析・ウェーブレット解析ガイダンス版：フーリエキングダムとウェーブレット革命    
                 
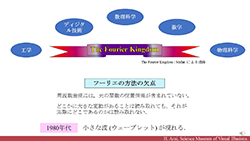  フーリエキングダム フーリエキングダムとウェーブレット革命    
  2021/11/6      
  フーリエキングダムとそのほころびを埋めたウェーブレットについて，信号処理の簡単な例も交えたトークです．
フーリエキングダムは S. マラーによる呼び方です         		  
   
   
                 
                 
                 
  第20回配信　          
  観てわかるLp空間の完備性とスモール lp 空間　Lp空間入門 No.2    
                 
  LP完備性 Lp空間入門 No.2    
  2021/9/28    
  完備性とLp空間の完備性を詳しく解説しました．Lp空間は関数解析、偏微分方程式論を学ぶ際にも必要となります。No.1と併せてご覧ください．  
   
   
                 
                 
                 
  第19回配信　            
  観てわかるLp空間とノルム空間　Lp空間入門 No.1       
                 
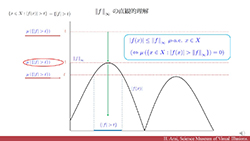  Lpノルム空間 Lp空間入門 No.1    
  2021/9/27・28       
  Lp空間の初歩を具体例を交えて丁寧に解説しました．この動画を見ているだけで証明まで知ることができます．ヘルダーの不等式やミンコフスキーの証明も説明します．           
   
   
                 
                 
                 
  第18回配信　        
  水彩錯視のパワポやグリーティングカードへの応用        
                 
  水彩錯視 水彩錯視のパワポやグリーティングカードへの応用    
  2021/9/4       
  水彩錯視の簡単な解説とその用途を考える。  
   
   
                 
                 
                 
  第17回配信　   
  正規直交基底と離散フーリエ変換の数学的基礎    
                 
  ONB 正規直交基底と離散フーリエ変換の基礎    
  2021/8/30       
  有限次元内積空間における正規直交基底の一般論からはじめ，特に離散フーリエ基底，離散フーリエ変換の数学的な基礎部分を，証明も含めて丁寧にわかりやすく解説します。
 
 
                 
                 
                 
  第16回配信        
  ウェーブレットへの誘い - ハール・ウェーブレットと多重解像度解析 -  
                 
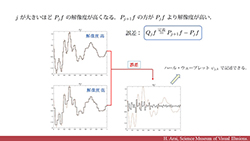  Wavelet ハール・ウェーブレットと多重解像度解析 
  2021/08/10 Ver.2      
  離散ウェーブレット解析で重要な多重解像度解析について，その考え方をハール・ウェーブレットを使って丁寧に説明します．また，連続ウェーブレット変換から離散ウェーブレット変換への移行にはどのようなメリットがあるのかを述べます．ウェーブレットの本格的な入門講義第２段です．   
 
 
                 
                 
                 
  第15回配信        
  ウェーブレットへの誘い - 窓付きフーリエ変換から連続ウェーブレット変換へ -  
                 
  Continuous Wavelet Transform 窓付きフーリエ変換から連続ウェーブレット変換 
  2021/07/15      
  ウェーブレットへの誘い，序章です。連続ウェーブレット変換についての入門講義をします。特に窓付きフーリエ変換の欠点を連続ウェーブレット変換がどのように補っているかを解説します。          
 
 
                 
                 
                 
  第14回配信        
  超関数とフーリエ変換入門   
                 
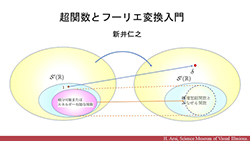  Distribution and Fourier Transform 超関数とフーリエ変換入門 
  2021/07/02      
  超関数って何？超関数のフーリエ変換ってどうするの？こういったことを知りたい方向けの動画です。シュワルツの超関数の理論により，古典的なフーリエ変換ができないような定数関数，ヘヴィサイド関数，ディラックのデルタ擬関数などのフーリエ変換も可能になります。この講義では，シュワルツによる超関数とフーリエ変換の理論の入門的な部分を，なるべくわかりやすく解説しました。
 
 
                 
                 
                 
  第13回配信       
  一般逆行列入門 - ムーア・ペンローズ一般逆行列，最小2乗解，多項式曲線によるデータ・フィッティング       
                 
  Generalized inverse 一般逆行列入門
  2021/06/18公開      
  一般逆行列の入門講義です。特にムーア・ペンローズ一般逆行列に焦点をあてて解説し，最小2乗解への応用，多項式曲線によるデータフィッティングへの応用について述べます。            
 
 
                 
                 
                 
  第12回配信       
  ダニエル積分とその使い方 - 確率論への応用        
                 
  Daniell integral ダニエル積分とその使い方 - 確率論への応用    
  2021/06/03公開       
  確率論や統計学では，与えられた分布をもつ独立確率変数の無限列がよく使われます．このような無限列の存在を保証する定理を一般化したものに角谷の定理があります．伊藤清先生がこの角谷の定理にダニエル積分を用いた別証明を与えています．この証明を本講義では，ダニエル積分とその使い方を述べつつ解説します．            
 
 
                 
                 
                 
  第11回配信        
  実解析と確率論 - マルチンゲール，ブラウン運動，実解析  
                 
  Brownian motion 実解析と確率論 - マルチンゲール，ブラウン運動，実解析    
  2021/05/28公開 ver.2 2023/5/22   
  実解析と確率論，特にマルチンゲールやブラウン運動とのよく知られた関係について初歩から丁寧に解説します．            
 
 
                 
                 
                 
  第10回配信        
  特異値分解入門 - 基礎から画像処理への応用まで -  
                 
  gazou1 特異値分解入門　- 基礎から画像処理への応用まで -    
  2021/4/30公開       
  行列の特異値分解は，最小2乗解，多変量解析，統計学，画像処理などさまざまな応用をもっています．この動画では線形代数の復習からはじめ，特異値分解の基礎から画僧処理への応用まで解説します．
 
 
                 
                 
                 
  第9回配信        
  ルベーグ集合とは - 実解析学講義 No.1 -    
                 
  gazou2 ルベーグ集合とは - 実解析学講義 No.1-    
  2021/4/25公開       
  「実解析的方法」は近年，偏微分方程式論，フーリエ解析，ウェーブレット解析，複素解析などでよく使われています．実解析学講義では，実解析的方法の基礎をわかりやすく解説します．No.1ではヴィタリの被覆補題を視覚的にわかりやすく解説し，ルベーグ集合について講義します．
 
 
                 
                 
                 
  第8回配信        
  ルベーグ測度とルベーグ積分  
  第1講　イメージがわかるルベーグ測度入門（ルベーグ測度の意味徹底解剖）       
                 
  ルベーグ測度 イメージがわかるルベーグ測度入門    
  2021/2/11公開       
  イメージがわかるようルベーグ測度の意味を徹底解剖しました．ルベーグ測度とルベーグ積分 第1講．
参考書：新井仁之「ルベーグ積分講義 -ルベーグ積分と面積0の不思議な図形たち」（日本評論社）．      
 
 
                 
  第2講　イメージがわかるルベーグ積分入門　－ルベーグ測度とルベーグ積分第2講
                 
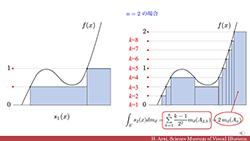  ルベーグ積分 イメージがわかるルベーグ積分入門    
  2021/2/11公開       
  イメージがわかるルベーグ測度入門（ルベーグ測度の意味を徹底解剖）に続く「ルベーグ測度とルベーグ積分」第2講です．ルベーグ積分の定義の丁寧な説明があります．
参考書：新井仁之「ルベーグ積分講義 -ルベーグ積分と面積0の不思議な図形たち」（日本評論社）．            
 
 
                 
                 
                 
  第7回配信        
  動画で学ぶフーリエ級数の収束定理．証明を読むのがしんどい方に．       
                 
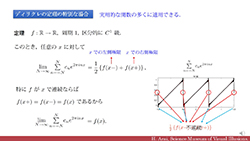  フーリエ級数 動画で学ぶフーリエ級数の収束定理．    
  2021/1/30公開       
  フーリエ解析で重要なフーリエ級数の各点収束に関する定理．使い勝手がよいものの証明はかなり面倒です．これを懇切丁寧に解説します．動画を見ながら自然に証明を学ぶことができます． 
所要時間：約32分          
 
 
                 
                 
                 
  第6回配信  
  微分積分入門 - エプシロン-デルタ論法 -  
                 
  エプシロン-デルタ論法 微分積分入門 - エプシロン-デルタ論法 -
  Ver.1 2020/12/22公開       
  微分積分入門篇としてエプシロン-デルタ論法を視覚的にわかりやすく解説します。
所要時間：約7分            
 
 
                 
                 
                 
  第5回配信            
  15分で証明も理解できる - 連続だが至る所微分不可能なワイエルシュトラス関数   
                 
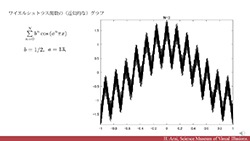  ワイエルシュトラス 連続だが至る所微分不可能なワイエルシュトラス関数    
  Ver.1 2020/12/21公開．改訂版 2021/1/25公開．
  連続かつ至る所微分不可能な関数として知られているワイエルシュトラス関数．この講義では至る所微分不可能であることをわかりやすく解説します．事実は知っていても証明を学んだことがないという人向けです．早稲田大学 教育学部 数学科で行った微積分のオンデマンド配信のオンライン授業の一部をもとにして数理科学デジタルオープンレクチャーズ用に新たに作成した講義動画です。
所要時間：約15分
 
 
                 
                 
                 
  第4回配信          
  超関数論への誘い - 15分でわかる超関数の考え方 一般・大学生向け        
                 
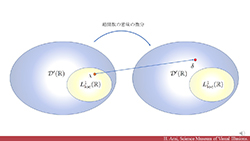  Distribution 超関数論への誘い - 15分でわかる超関数の考え方    
  Ver.1 2020/11/3公開       
  超関数は偏微分方程式論，フーリエ解析，ウェーブレット解析，あるいは信号解析の数学的研究などにも顔を出す便利な理論です。この動画では超関数の考え方をできるだけわかりやすく説明していきたいと思います．
所要時間:：約15分。
 
 
                 
                 
                 
  第3回配信          
  掛谷予想入門  一般・大学生向け  
                 
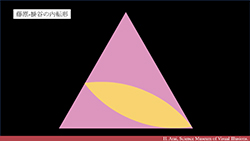  Kakeya conjecture1 No.1 掛谷予想の前哨戦 - 掛谷予想が生まれる背景 
  Ver.1　2020/10/29公開       
  掛谷による問題の発端は果たして「武士が厠で槍を一回転させるのに必要なスペースを見つける」からきているのか？このエピソードの真相に独自の調査で迫ります。また、掛谷，藤原，窪田の結果をもとに作成したオリジナル動画で掛谷による問題を説明します。所要時間：約14分。
 
 
                 
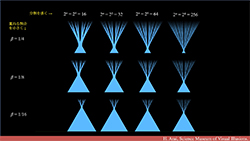  Kakeya conjecture2 No.2 ベシコヴィッチの定理とベシコヴィッチ・モンスター    
  Ver.1 2020/10/29公開       
  掛谷問題に絡む驚くべき定理です。ベシコヴィッチモンスターをオリジナル動画で図解します。所要時間：約9分。
 
 
                 
  Kakeya conjecture3 No.3 掛谷予想とハウスドルフ次元 
  Ver.1 2020/10/29公開       
  「掛谷問題」と呼ばれる未解決問題（No.1の掛谷による問題に端を発するが、それとは異なる）を述べ、現在どこまで解明されているのかを解説します。ブルガンやタオらの結果も紹介します。 ハウスドルフ次元入門付き。
所要時間：約15分。   
 
 
                 
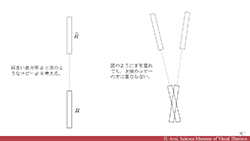  Kakeya conjecture4 No.4 多変数フーリエ解析と掛谷予想    
  Ver.1 2020/10/29公開       
  1971年、フェファーマンがベシコヴィッチモンスターを使いフーリエ解析の新たな地平を開きました。掛谷問題と偏微分方程式論、解析数論の未解決問題との関係も見出されています。フーリエ解析Quick入門の後、掛谷問題の広がりを見ていきます。所要時間：約14分。
 
 
                 
                 
                 
  第2回配信            
  画像処理の数学 - フーリエの方法篇 一般・大学生向け　  
                 
  image processing1 No.1　画像と線形空間    
  所要時間：約10分。    
           
           
           
                 
  image preocessing2 No.2　離散コサイン基底       
  所要時間：約8分。    
           
           
           
                 
                 
    No.3　離散コサイン基底と画像圧縮　近日公開       
    No.4　フーリエ基底とディジタルフィルタ　近日公開  
       
    続編：画像処理の数学 - ウェーブレット篇  
                 
                 
  第1回配信            
  動画で学ぶフラクタル - 自然数でない次元の世界を垣間見る　一般・高校生向け
                 
  画像１ No. 1　イントロダクション：コッホの雪片曲線   
  所要時間：約9分。    
           
           
           
                 
  Fractal No. 2　様々な自己相似集合     
  所要時間：約9分。    
           
           
           
                 
                 
  外部リンク            
  新井仁之　マイポータル reseachmap    
                 
  本ページに記載の文章、画像、動画の一部あるいは全部の無断転載、複写、複製することを禁じます。   
  ©2020 Hitoshi Arai. All rights reserved.  
                 
      ---------