キャッシュをご覧になっている場合があります．更新して最新情報をご覧ください．
                 
  ルベーグ積分講義　講義動画集  
                 
  早稲田大学教授/東京大学名誉教授  
  新井仁之  
                 
  数学書を一人で読んでいながら、教室での講義も聴いているような感じのする動画を作成してあります。
本の予習、復習、まとめの補助としてもお役に立てるはずです。
本書と併せて講義動画をご視聴ください。            		  
                 
                 
   
ルベーグ積分講義  [改訂版]  - ルベーグ積分と面積0の不思議な図形たち    
  日本評論社 2023年5月刊  
                 
  訂正情報（2024/4/12更新）         
    こちらからご覧ください       
                 
                 
  その他の情報             
    ルベーグ積分のアルゴリズムによる近似計算のプログラム       
                 
                 
      講義動画一覧      
   
  ルベーグ積分に関するオンライン講義動画（制作：新井仁之）です。『ルベーグ積分講義 [改訂版]』を読む際の参考にしてください。各動画の画像をクリックすると動画をご覧いただけます。証明などの詳細は上記の『ルベーグ積分講義 [改訂版]』にあります。  
                 
                 
  ルベーグ測度        
                 
  イメージがわかるルベーグ測度入門（ルベーグ測度の意味
  を徹底解剖）  
  所要時間：約30分   
  イメージがわかるようルベーグ測度の意味を徹底解剖しました．『ルベーグ積分講義 [改訂版]』の第1章から第6章のアウトラインをアニメーションを交えてわかりやすく解説してあります。
 
                 
                 
  ルベーグ積分     
                 
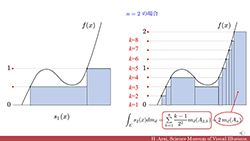  ルベーグ積分 イメージがわかるルベーグ積分入門    
  所要時間：約21分   
  ルベーグ積分の定義の丁寧な説明とルベーグの収束定理、フビニの定理の解説があります．『ルベーグ積分講義 [改訂版]』 の第7章、第8章、第9章、第11章のエッセンスをご覧いただけます。     
 
 
                 
                 
  Lp空間入門 No.1            
             
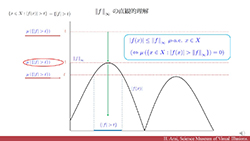  LP 観てわかるLp空間とノルム空間    
  所要時間：約33分   
  『「ルベーグ積分講義 [改訂版]）』第10章の解説動画となっています。            
 
 
                 
                 
  Lp空間入門 No.2          
                 
  LP No2 観てわかるLp空間の完備性とスモールlp空間    
  所要時間：約21分  
  『ルベーグ積分講義 [改訂版]』第10章の解説動画となっています。
 
 
                 
                 
  微分同相写像によるルベーグ積分の変数変換の公式       
                 
  微分同相写像によるルベーグ積分の変数変換の公式    
  所要時間：約39分   
  『ルベーグ積分講義 [改訂版]』第13章の解説動画です。本をテキストにして講義を視聴すると、証明の理解を助けます。新作｡          
 
 
                 
                 
  掛谷問題の周辺  
                 
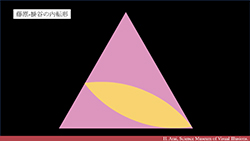  Kakeya conjecture1 No.1 掛谷予想の前哨戦 - 掛谷予想が生まれる背景 
  所要時間：約14分  
  掛谷による問題の発端は果たして「武士が厠で槍を一回転させるのに必要なスペースを見つける」からきているのか？このエピソードの真相に独自の調査で迫ります。また、掛谷，藤原，窪田の結果をもとに作成したオリジナル動画で掛谷による問題を説明します。
 
 
                 
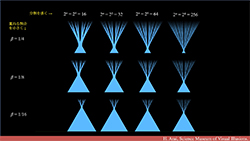  Kakeya conjecture2 No.2 ベシコヴィッチの定理とベシコヴィッチ・モンスター    
  所要時間：約9分
  掛谷問題に絡む驚くべき定理です。ベシコヴィッチモンスターをオリジナル動画で図解します。証明は「ルベーグ積分講義[改訂版]」第15章参照。
 
 
                 
  Kakeya conjecture3 No.3 掛谷予想とハウスドルフ次元 
  所要時間：約15分
  「掛谷問題」と呼ばれる未解決問題（No.1の掛谷による問題に端を発するが、それとは異なる）を述べ、現在どこまで解明されているのかを解説します。ブルガンやタオらの結果も紹介します。 ハウスドルフ次元入門付き。ハウスドルフ測度とハウスドルフ次元に関する詳細は「ルベーグ積分講義[改訂版]」第16章・第17章参照。 
 
 
                 
  Kakeya conjecture4 No.4 多変数フーリエ解析と掛谷予想    
  所要時間：約14分
  1971年、フェファーマンがベシコヴィッチモンスターを使いフーリエ解析の新たな地平を開きました。掛谷問題と偏微分方程式論、解析数論の未解決問題との関係も見出されています。フーリエ解析Quick入門の後、掛谷問題の広がりを見ていきます。
 
 
                 
  『掛谷予想（掛谷問題）入門』は早稲田大学で行ったオンライン授業を基にして作成した動画です。 
                 
                 
  フラクタル - 自己相似集合
                 
  画像１ フラクタル No.1 イントロダクション：コッホの雪片曲線  
  所要時間：約9分
  『ルベーグ積分講義 [改訂版]』第17章で解説したコッホ曲線の作り方の動画です。    
           
           
                 
  Fractal フラクタル No. 2　様々な自己相似集合     
  所要時間：約9分
  さまざまな自己相似集合の作り方が動画解説してあります。 『ルベーグ積分講義 [改訂版]』第17章の参考にしてください。 
           
           
                 
                 
  確率論、その他          
  『ルベーグ積分講義 [改訂版]』第18章に続く動画です｡       
                 
  実解析と確率論- マルチンゲール、ブラウン運動、実解析    
  所要時間：約35分       
  マルチンゲールや2次元ブラウン運動の古典調和解析への応用を概説してあります。この動画と併せて次の動画もご覧ください。
 
           
                 
  ルベーグ集合とは    
  所要時間：約35分       
  『実解析と確率論』の関連動画。併せてご覧ください。ルベーグの微分定理、ルベーグ集合、ヴィタリの被覆補題などを非常にわかりやすく解説しております。      
 
           
                 
                 
  ダニエル積分とその使い方　確率論への応用    
  所要時間：約32分       
  『ルベーグ積分講義 [改訂版]』第18章で学ぶホップの拡張定理ではなく、伊藤清『確率論』(1963)に基づき、ダニエル積分を使って独立確率変数の無限列の存在を示しています。            
 
 
                 
                 
                 
                 
      ルベーグ積分講義関連リンク      
                 
    「改訂版 はじめに」がWeb日本評論から読めます。       
                 
    数理科学デジタルオープンレクチャーズ     
  ここで挙げた動画の他、さまざまな分野の講義動画をご覧いただけます。