illusion	museum	illusion art	mathematics	Science Museum of Visual Illusions, Japan
					Tweet
					Japanese Version
THE BIRTH OF "NEW AGE OP ART"
New Op Art born from Mathematical Science of Optical Illusions
- An Exhibition of Works of Hitoshi Arai and Shinobu Arai -
	Since Dec. 27, 2011
	Hitoshi Arai (Prof. Emeritus at Univ. of Tokyo from 2020)
	Currently I am a professor of mathematics at Waseda University, Japan (from Apr., 2018). I have studied about visual perception by mathematical methods. My aim is to establish a new discipline, mathematical vision science. Here I would like to show you my works of visual illusions which are by-products of my study of mathematical models of visual information processing in the brain. All works I will exhibit here were produced jointly with Shinobu Arai.
AREA 1. An Algorithm for Making Fuyuu Illusions - New Technique Creating a New Age of Optical Art.
	(*) Fuyuu is a Japanese word which means "waft" or "float".
Fig.1.1. Wreath Motion Illusion - The Birth of New Age Op Art  ©Hitoshi Arai and Shinobu Arai, Dec. 21, 2011.
		How to see the illusion. Please look at the small disc in the centre of the picture. Then please bring your head close to the picture, subsequently keep away your head from it, and repeat this action. You will feel that the wreath moves circularly on the picture although it is a still image.
	I invented with S. Arai an algorithm for making fuyuu illusion (US Patent). Fig. 1.1 was made by using the algorithm. So far, motion illusions were made by special talented researchers or designers by using simple patterns: for example, Ouchi illusion, Pinna illusion, Gurnsey-Morgan illusion, and Kitaoka's illusions, etc.. However our algorithm can transform any pictures to certain motion illusions! This algorithm is based on our mathematical (neural) model of visual information processing in the brain: we elucidated mathematically a neural mechanism producing certain motion illusions (fuyuu illusions).
	Next I will show you other works made by our "algorithm for making fuyuu illusions".
	Fig. 1.2. Jumping Rabbit Motion Illusion. Copyright Hitoshi Arai and Shinobu Arai, Jan. 1, 2011
		Please see the picture by the same manner as Fig.1.1..
	This year, 2012, is the year of the Dragon in terms of the Oriental zoadic. I made with S. Arai the following illusion for celebrating happy new year. Please see the picture by the same manner as Fig.1.1.
	Fig. 1.3 Dragon and Ball Illusion. A dragon is just about to grip a glittering ball.
	Our algorithm of making fuyuu illusions is able to produce fuyuu illusions not only from handwriting designs but also photos. The following Fig. 1.4, and 1.5 are fuyuu illusions made from pictures of flowers.
Fig 1.4. Flower Fuyuu Illusion
	How to see the illusion. Please move the picture up and down (resp. to the right and to the left) slowly and smoothly. Then you feel that flowers waft to the right and to the left (resp. up and down).
Fig. 1.5 Flower Garden Fuyuu Illusion
		How to see the illusion. Same as Fig. 1.1.
The following is also obtained by our fuyuu illusion algorithm.
Fig. 1.6 Beating Fuyuu Heart Illusion
		How to see the illusion. Please see the picture moving slowly your head from diagonally above to below and then from diagonally below to above. Repeat this action. You feel that a big heart and small harts in it slide on the picture. Please bring your head close to the picture, subsequently keep away your head from it, and repeat this action. Then you perceive like a big heart is beating.
An Extra. Herald Motion Illusion. Copyright Hitoshi Arai and Shinobu Arai, Nov. 6, 2010.
		How to see the illusion. Please move the picture up and down slowly and smoothly. Then you feel that Japanese character strings waft to the right and to the left. The pronunciation of the character string is "Sakigake". This means "Precursory Research for Embryonic Science and Technology", the name of a reseach project which supported my study of visual perception.
AREA 2. Hyperbolic Illusions   - Illusion art which was born from neurophysiology -
	I and Shinobu Arai found a class of illusions by a neuro-physiological speculation. We call illusions in the class hyperbolic illusions. The following is one of hyperbolic illusions:
Fig.2.1. Hyperbolic Illusion of Fraser Type. Copyright Hitoshi Arai and Shinobu Arai, 2010.
		Bended Fraser's twisted cords which are arrayed along rectangular hyperbolic coordinate axes (see below) seem to tilt anti-clockwise.
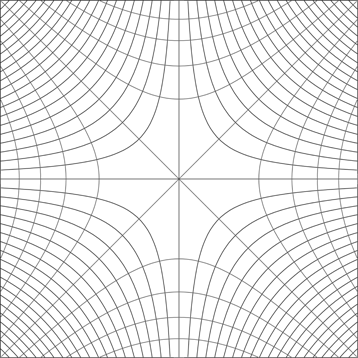	Fig.2.2. Rectangular hyperbolic coordinates (not illusion).
	Fig. 2.3. Two hyperbolic illusions of Fraser type. Copyright Hitoshi Arai and Shinobu Arai, 2010.
	For details and for mathematical study of other geometrical illusions, please see the following research paper:
		[1] Hitoshi Arai and Shinobu Arai, Framelet analysis of some geometrical illusions, Japan J. Indust. Appl. Math. 27 (2010), pp.23-46. (pdf available)
AREA 3. Fractal Spiral Illusions   - Fractal geometry meets illusion art -
	We produced a spiral illusion from a fractal pattern:
Fig.3.1. Fractal Spiral Illusion. Copyright Hitoshi Arai and Shinobu Arai, 2007.
		The above picture consists of copies with various sizes of a well known self-similar set called the fractal island (see Fig. 3.2). When you see the fractal spiral picture (Fig. 3.1), you will perceive that fractal islands form an anti-clockwise spiral. However actually the islands are arrayed like concentric circles.
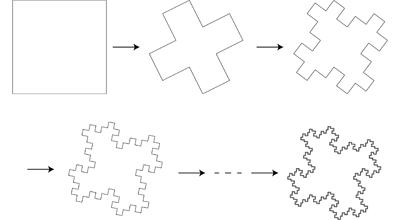	Fig. 3.2. How can we get the fractal island ?
	Fractal spiral illusions is one of spiral illusions, and it has greater illusion magnitude. As is well known, the most old spiral illusion is the Fraser spiral illusion. However, the fractal spiral illusion has different properties from the Fraser spiral illusion. I would like to describe them. First is as follows.
	Fig. 3.3. Distorted Circle Illusion. Copyright Hitoshi Arai, 2009.
	Please see the above picture. Greened concentric circles seem to be distorted on the fractal spiral illusion. On the other hand, J. Fraser showed in his paper in 1908  ("A new visual illusion of direction") illusions that some concentric circular, modified twisted cords seem to be warped. However there is a difference between Fraser’s distorted circle illusions and ours. It is that the circles in Fig. 3.3 is not twisted cords, but only circled lines.
	I would like to point out another inherent feature of the fractal spiral illusion. Please see the following colored fractal spiral picture:
	Fig. 3.4. Colored Fractal Spiral Illusion. Copyright Hitoshi Arai and Shinobu Arai, 2010.
	You will perceive spiral illusion. However when the color is changed as follows, you don't recognize spiral illusion in Fig. 3.5:
Fig. 3.5. Colored Fractal Spiral Picture without Illusions. Copyright Hitoshi Arai and Shinobu Arai, 2010
	However this phenomenon does not happen in the case of the Fraser sipral illusion whose color is changed as in Fig. 3.5:
	Fig. 3.6. Colored Fraser's spiral illusion. Copyright HItoshi Arai and Shinobu Arai, 2010.
AREA 4. Tilt illusions constructed by character strings.
	Around 2005, many incogniti put up onto electronic Japanese bulletin boards several tilt illusions constructed by Japanese charcter strings. H. Arai and S. Arai named them "Mojiretsu Keisya illusions" which means tilt illusions constructed by character strings. For simplicity, we abbreviate mojiretsu keisya illusions to MK illusions.
	We reported our mathematical study of MK illusions in two articles in Japanese. By using the mathematical method described in the papers, we find several MK illusions. For example,
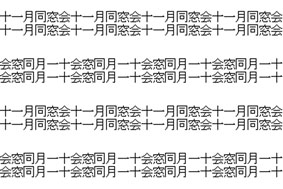Fig. 4.1. November Alumni Union Illusion. Copyright Hitoshi Arai and Shinobu Arai, 2009.
		Slant Japanese strings are arrayed actually mutually parallel. The Japanese word in the above picture means "An alumni reunion is held in November".
	We can make MK illusions not only by using characters but mathematical formulas.
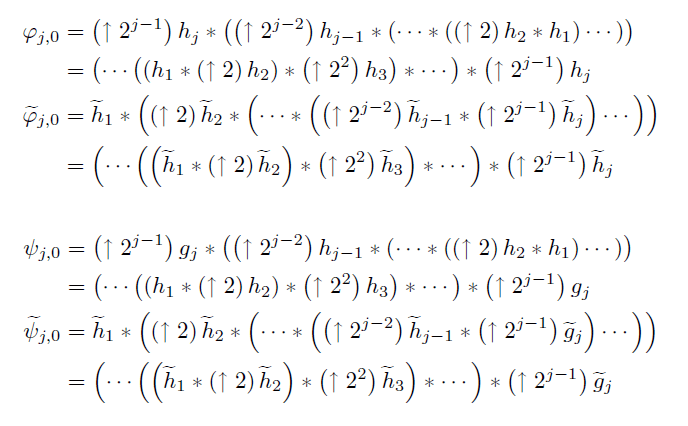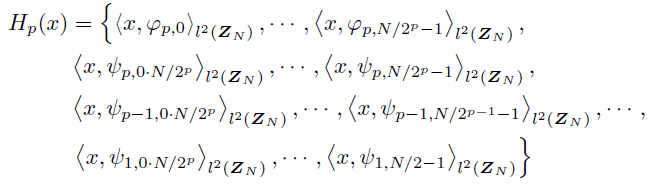	Fig. 4.2. Mathematical Tilt Illusions. Copyright Hitoshi Arai, 2010.
	What are they? These are real mathematical fromulas. They are from my text book "Wavelets" (Kyoritsu Publ. Japan, 2010).
AREA 5. Mathematical vision science established the first method of controlling magnitudes of illusions in the world !
	By using above mentioned mathematical formulas (which are tilt illusions) and other mathematics, I analyzed several tilt illusions. As a result, I and S. Arai succeeded in identifying illusory factors of certain tilt illusions. If the illusory factor is subtracted from a tilt illusion, then we obtain an image which gives us no illusiory impression. For example, the following image is the result of subtraction of illusory factor from Fig. 4.1:
Fig. 5.1. Removal of the illusory factor from Fig. 4.1. Copyright Hitoshi Arai and Shinobu Arai, 2009.
	We can apply our method to other tilt illusions (for example, the cafe wall illusion). For details, see
		[2] H. Arai and S. Arai, VISION - J. Vision Soc. Japan-, 17 (2005), 259-265.
	Moreover, by modifying the method for tilt illusions we can remove illusory factors from more general geometrical illusions (H. Arai and S. Arai [1]). Here is an example: Fig. 5.2 is the fractal spiral illusion, and Fig. 5.3 is the result of subtracting illusory factor. We cannot perceive any spiral illusion in Fig. 5.3.
Fig. 5.2. Fractal Spiral Illusion					Fig. 5.3. Removial of illusory factors.
Copyright Hitoshi Arai and Shinobu Arai, 2007.					Copyright Hitoshi Arai and Shinobu Arai, 2010.
	As described in H. Arai and S. Arai [1], the fractal spiral illusion consists of illusory factors, anti-illusory factors, mixed-illusory factors, and non-illusory factors. Fig. 5.3 is obtained by removing illusory, anti-illusory and mixed-illusory factors. If we remove only anti-illusory factors, then we have the following stronger illusion:
	Fig. 5.4. Stronger Fractal Spiral illusion. Copyright Hiotshi Arai and Shinobu Arai, 2010.
AREA 6. Variations of Classical Illusions by Mathematical Method.
	The following two pictures are variations of the Fraser spiral illusion. Several twisted cords are arrayed like concentric circles. However with the help of fringes, twisted cords look like stream lines of a viscous fluid. Can you describe the flow of the fluid ?
Fig. 6.1. Fluid Mechanical Fraser Illusion 1. Copyright Hitoshi Arai and Shinobu Arai, Dec.30, 2011.
Fig. 6.2. Fluid Mechanical Fraser Illusion 2. Copyright Hitoshi Arai and Shinobu Arai, Dec.30, 2011.
AREA 7. 3D Illusions Everywhere
	In this area I will show you illusions which I found in towns in Japan. Please enjoy the pictures not as art, but 3D illusions.
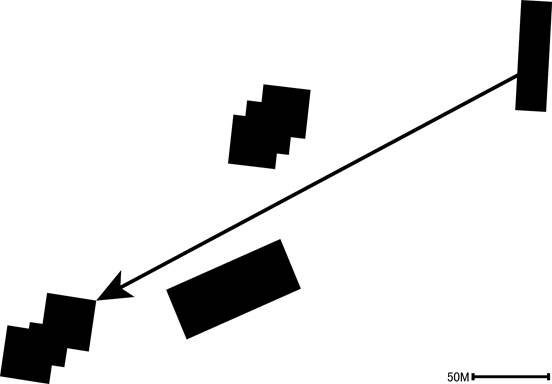
	The following pictures (Fig. 7.1 and 7.2) are scenes in Osaka city. You can find 3 buildings in Fig. 21 (or Fig. 22). Do you feel that the building at center (the Ritz-Carlton Osaka) is placed more forward than the left and right buildings ? However, it is in fact about 50 meters behind the left bldg. and about 100 meters behind the right bldg. (see Fig.7.3).
	Fig. 7.1. A Three Dimensional Illusion in Osaka. Copyright Hitoshi Arai, 2009.
		Left: Breeze Tower. Center: the Ritz-Carlton Osaka. Right: Herbis Ent Office Tower.
	Fig. 7.2. A Three Dimensional Illusion in Osaka. Copyright Hitoshi Arai, 2009.
	Fig. 7.3 Map (outline). Fig. 7.1 and Fig. 7.2 were photographed from the Hilton Osaka.
	Fig. 7.2 was published in a textbook on mathematics for junior high school !
	I found the following illusion in Kanazawa city in Japan.
	Fig.7.4. A Three Dimensional Illusion in Kanazawa. Copyright Hitoshi Arai, Oct. 2011.
		"B" seems to be a part of the brown building next to the hokkoku kaikan building. However "B" is a part of the hokkoku kaikan building.
	E-mail
	Copyright 2011 by Hitoshi Arai. All rights reserved. No part of this site may be reproduced or transmitted in any form or by any means.
About Science Museum of Visual Illusions, Japan.
	Science Museum of Visual Illusions, Japan is a virtual museum. Please visit our museum.
Sorry, all explanations of illusions in the museum are in Japanese. English version is in preparation.
Illusion, Museum, Illusion Arts, Mathematics are our Key Words.