目の錯覚と魔法の数学			錯視	錯覚	渦巻き錯視	フラクタル	数学	視覚
	Web 連載						- 第 1 回-
					東京大学教授　新井仁之
	みなさんは小学校では算数、中学からは数学を勉強してきました．そのとき，こんなことを思いませんでしたか？
							？
		数学って面白くない．何の役に立つのだろう？
	でも，数学ってとても面白いんですよ．それにいろいろなことに使えます．誰も思いもよらないようなこともできるのですよ．
	ここでは，数学を使って目に錯覚を起こさせたり，取り除いたり，まるで数学が魔法のように働くことをお見せしましょう．
	目の錯覚のことを錯視といいます． 錯視にはいろいろなタイプのものがあります．まずはその中の『渦巻き錯視』と呼ばれている錯視のお話しから始めます．
	渦巻き錯視が作られたのは今からおよそ100年前になります．イギリスの心理学者 James Fraser が1908年にフレーザー錯視，あるいはフレーザーの渦巻き錯視と呼ばれているものを発表しました．それは次のような図形です．
	フレーザーの渦巻き錯視
	（ただし上図はフレーザー錯視を元にMatlabで描画したもの）
	この図の黒と白のねじれたひもが中心に向かって反時計回りに渦巻いているように見えませんか．しかし，それは目の錯覚によるもので，本当は黒と白のねじれたひもは同心円になっているのです！
	そう言われても，にわかには信じられないかもしれません．  しかし黒と白のねじれたひもを指でなぞってみると，驚くべきことに確かにらせんではなく，円になっていることが確認できると思います．
	渦巻き錯視はフレーザーの1908年の論文以降，研究が進められました．中でも日本の心理学者，北岡明佳さんらの研究はたいへん注目すべきものです．それについては，また後で述べることにして，ここでは数学に話を向けましょう．
	皆さんは
			フラクタル幾何学
	という言葉をお聞きになったことがありませんか．
	フラクタル幾何学というのは，例えば複雑な海岸線のように細部に至るまでごちゃごちゃとしているような図形を研究する数学の一分野です．特に，単純なパターンの操作を繰り返して作られる人工的なフラクタル図形を自己相似集合といい，フラクタル幾何学の重要な研究対象になっています．単純な操作の繰り返しなのに，これが不思議なことに自然界に存在するものの形状に類似したものになっていることもあるのです．
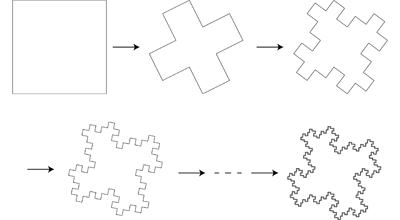
	今回は「フラクタル島」と呼ばれている次のようなパターン操作の繰り返しでできる自己相似集合に着目します．
	この図だけだと少しわかりにくいと思いますので，もう少しわかりやすい次のアニメーションをご覧いただきましょう．
	フラクタル島の形成 アニメーション
	このフラクタル島を少し縦長にして同心円状に配列すると，驚くべきことに次のような渦巻き錯視ができることを私と共同研究者の新井しのぶは発見しました．この錯視を錯視研究で有名な北岡明佳さんに見ていただいたところ，早速『フラクタル螺旋錯視』と命名してくれました．
		フラクタル螺旋錯視 (新井・新井 2007)
	フラクタル螺旋錯視は非常に錯視量が多い渦巻き錯視です．実際，渦巻きが急速に中心に向かっているように知覚されます．
	このように数学が新しい錯視図形の作成に役立つこともあるわけです．
	しかし，これはほんの序の口．数学の力はもっとすごいのです．次回はそれをお見せしましょう．
			チャプターリスト
		第 2 回
履歴　第1版　 2010年7月1日
本文および図版の無断転載・複製を禁止します．