| 悪魔の階段 |
|
|
カントル集合 |
|
錯視の科学館 展示 |
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
Not visual illusions |
|
|
|
| |
A Recipe for Making Cantor Devil's Staircase |
|
| |
|
| |
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
Hitoshi Arai and Shinobu Arai |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
感覚的にはありえないにもかかわらず,数学的には存在することがあります.その一つの例である「カントルの悪魔の階段」を階段らしく描いてみました. |
|
| |
|
|
|
|
|
|
|
|
 |
| |
3D版カントルの悪魔の階段(新井仁之・新井しのぶ) |
|
| |
|
|
|
|
|
|
|
|
| |
この階段は日常的な感覚とはかなりズレているものです.それを見るために,カントルの悪魔の階段の断面図を描いてみます. |
|
| |
|
|
|
|
|
|
|
|
 |
| |
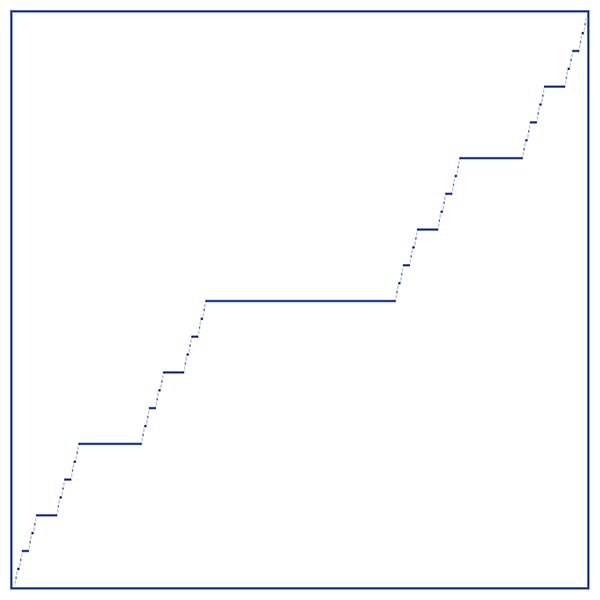
カントルの悪魔の階段 |
|
| |
|
|
|
|
|
|
|
|
| |
これがもともとカントルの悪魔の階段と呼ばれているもののグラフです.この関数の不可思議な点は次のようところです.[0,1] 上の連続関数 y=f(x) が,もしも至る所で平坦であれば,すなわち微分係数が f'(x)=0 となっていれば f(x) は定数になっています.しかし,カントルの悪魔の階段は,おおざっぱに言えば,確率 1 で平坦であるにもかかわらず,f(0)=0 から f(1)=1 へと変化していく連続関数なのです. |
|
| |
言い換えれば,確率 0 でしか変化していないにもかかわらず,0 から 1 へと変化しているのです. |
|
| |
|
|
|
|
|
|
|
|
| |
最後にカントルの悪魔の階段の作り方を動画で御覧頂きましょう.この動画は有限回の操作で終わっていますが,実際はエンドレスで,無限回続きます. |
|
| |
|
|
|
|
|
|
|
|
|
| A recipe of making Cantor Devil's Staircase (Hitoshi Arai and Shinobu Arai,
2002) |
| |
カントルの悪魔の階段の描き方(新井仁之・新井しのぶ,2002年) |
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
カントルの悪魔の階段については, |
|
| |
新井仁之,ルベーグ積分講義 - ルベーグ積分と面積0の不思議な図形たち -,日本評論社,2003 |
|
| |
をご参照ください. |
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
本ページの一部・全部の無断転載・複写を禁じます. |
|
|
| |
錯視の科学館の外部からアクセスしている方は,次をクリックしてください.錯視の科学館入口です |
|
| |
|
|
 |
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|