| ���� | �J�t�F�E�H�[������ | �w�I���� | �t���[�U�[�����@ �~�����X�^�[�x���N���� | |||||
| �����̉Ȋw�� | ||||||||
| �w�I�����̍\���̉� (1) | ||||||||
| �J�t�F�E�H�[�������ƌX������ | ||||||||
| - �J�t�F�E�H�[�������ȂnjX�������̍\���𐔊w�I�ɉ𖾂��� - | ||||||||
| 2010�N12��16��(�����e) | ||||||||
| 2015�N12��9���i�����e�j | ||||||||
| ������w��w�@�����Ȋw�����ȁ@�V��m�V | ||||||||
| (���F2018 ��葁��c��w�Ɉڐ�) | ||||||||
|
|
||||||||
| �T�v�@�w�I�����̈�ɌX������������܂��D�����ł͂܂��X�������̑�\��̈�ł���J�t�F�E�H�[�������̃��J�j�Y������͂��܂��D���ɃJ�t�F�E�H�[�������ƃt���[�U�[�̂˂���R�̊֘A�����m�ɂȂ�Ǝv���܂��D ����ɂ��̑��̌X�������ɂ��Ă����l�̉�͂��s���܂��D�{�y�[�W�͕M�҂̘_�� [1]�C[2]�œ���ꂽ���ʂ̉���ł��D | ||||||||
|
|
||||||||
| 1. �J�t�F�E�H�[������ | ||||||||
| ���̐}���������������D���������ɃO���[�̐�������܂����C�����݂͌��Ⴂ�ɌX���Ă���悤�Ɍ����܂��D���������̂悤�Ɍ�����͍̂��o�ŁC���ۂ͕��s�ɔz�u����Ă���̂ł��D ������u�J�t�F�E�H�[�������v�Ƃ����܂��D | ||||||||
 |
||||||||
| �J�t�F�E�H�[������ (Gregory-Heard, Fraser) | ||||||||
| �J�t�F�E�H�[���Ƃ����̂̓J�t�F�̕ǂƂ����Ӗ��ł��D�Ȃ�����Ȗ��O�����Ă���̂��Ƃ����ƁC���̃f�U�C�����u���X�g���̃J�t�F�̕ǂɂ��������Ƃɂ��܂��D���̃J�t�F�̎ʐ^�̓J�t�F�E�H�[�������Ɋւ���ÓT�I�Ș_�� | ||||||||
| {GH] R. L. Gregory and P. Heard, Border locking and the Cafe Wall illusion, Perception, 8 (1979),365-380 | ||||||||
| �Ɍf�ڂ���Ă���̂ŁC�����̂�����͂������������F | ||||||||
| http://www.richardgregory.org/papers/cafe_wall/cafe-wall_p1.htm (Gregory����HP) | ||||||||
| �@�Ȃ��C�J�t�F�E�H�[�������̑�ꔭ���҂̓O���S���[�ł͂���܂���D���߂ɂ���悤�Ƀt���[�U�[��������ȑO�ɘ_���Ă��܂��i�k���w��������x�Q�Ɓj�D�������C����ɂ���ȑO�ɂ���C�ۊw�҂ɂ�����Ă��邱�Ƃ��C�V��E�V��̒����ɂ�蔭������܂����D�ڂ����͉��L�̘_�� | ||||||||
| �V��m�V�E�V�䂵�̂ԁw�e���v���E�E�H�[����������J�t�F�E�E�H�[�������� - �J�t�F�E�E�H�[���E�^�C�v�̍�����1893�N�ɔ�������Ă���- �@From the Temple Wall Illusion to the Cafe Wall Illusion - A Cafe Wall type illusion was discovered already in 1893 - �x | ||||||||
| ���������������D | ||||||||
| ���āC�{��ɖ߂�C���̖��ɂ��Ę_���邱�Ƃɂ��܂��傤�D | ||||||||
| �J�t�F�E�H�[�������͂ǂ̂悤�Ȃ��Ƃ��v���ŋN����̂ł��傤���H | ||||||||
| 2. �J�t�F�E�H�[�������ƃt���[�U�[���� | ||||||||
| �@Gregory��̘_�����o�ł����70�N�O�CJ. Fraser�Ƃ����l���X��������Q���������Ɋւ���_�� | ||||||||
| [F] J. Fraser, A new visual illusion of direction, British J. Psychology 2 (1908), 307-320. | ||||||||
| �\���܂����D���̒���Fraser�̓~�����X�^�[�x���O���� (�J�t�F�E�H�[�������摜�̃O���[�̐������������^�C���Ɠ������ɂ�����) �Ǝ��ɐ}������t���[�U�[�����Ƃ̊֘A���w�E���Ă��܂��D(�Ȃ����̘_�����ŁA�t���[�U�[�͐��������O���[�̏ꍇ�A���Ȃ킿�J�t�F�E�H�[�������ɂ��Ă����łɘ_���Ă��܂��B) | ||||||||
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ |
���F���}��Fraser�̘_���̐}���̂��̂ł͂Ȃ��C�k���������ɂ��f�U�C���Ɋ�Â���Matlab���g���č�悵�����̂ł��D | |||||||
| �t���[�U�[���� (Fraser) | ||||||||
| �����ɕ���ł���˂��ꂽ�R�̂悤�ȃf�U�C�����X���Č����Ă���Ǝv���܂��D���������ۂɂ͂���͕��s�ɔz��Ă��܂��D �R�̎���ɏ��肪���Ă܂����C�������苎��Ǝ��̂悤�ɂȂ�܂��D | ||||||||
 |
||||||||
| ����Ȃ��̃t���[�U�[�����iFraser�j | ||||||||
| �~�����X�^�[�x���O�������邢�̓J�t�F�E�H�[�������ƁC���̂˂���R�̍����Ƃ͂ǂ̂悤�ȊW������̂ł��傤���D�����ł͐G��܂��CFraser�̘_���ł́C���̊W��}������}�ł��L����Ă��܂��D���͋����[�����Ƃ́CFraser�̘_�����炨�悻80�N��Ɍ��ꂽMorgan��Moulden�̎��̘_���Ŏ����ꂽ���Ƃł��D | ||||||||
| [MM] M.J.Morgan and B. Moulden, The Munsterberg figure and twisted cords, Vision Res. 26 (1986), 1793-1800 | ||||||||
| ���̘_���ŁCMorgan��Moulden�́C����ш�ʉ߃t�B���^ �ŃJ�t�F�E�H�[�������摜���t�B���^�����O����Ƃ˂���R��̃p�^�[��������邱�Ƃ��������̂ł��D | ||||||||
| �@�����Ŗ�肪�����܂��D�m���ɑш�ʉ߃t�B���^�ɂ��t�B���^�����O�ł˂���R��̃p�^�[��������܂����C����ł́C | ||||||||
| ���̂˂���R��̃p�^�[�����{���ɃJ�t�F�E�H�[�������̌����ɂȂ��Ă���̂ł��傤���H | ||||||||
| 3. �J�t�F�E�H�[�������Ƃ˂���R��̃p�^�[���@(�V��E�V��[1]) | ||||||||
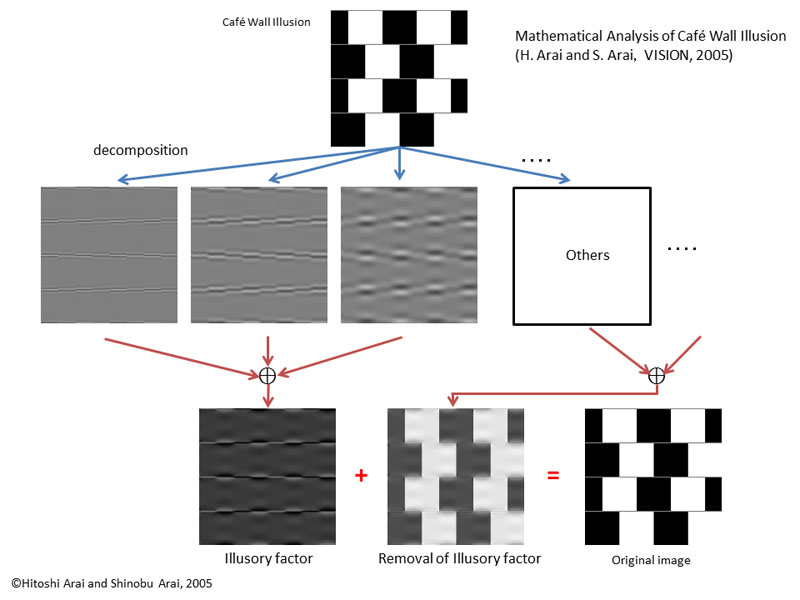
| �@�M�҂�̓J�t�F�E�H�[�������}�`��o�����E�F�[�u���b�g�ɍő�d���@��g�ݍ��킹�ĉ�͂��Ă݂܂����D ���ʂ͉��̕\�̂悤�ɂȂ�܂����D | ||||||||
 |
||||||||
| �}1 | ||||||||
| �}�P�̐������������܂��C�܂��J�t�F�E�H�[��������o�����E�F�[�u���b�g�ɂ��ő�d�����d�𑜓x�������܂��D�o�����E�F�[�u���b�g�ƍő�d�����d�𑜓x�����ɂ��Ă͔���ƌ����̉����ʂɗ\�肵�Ă܂����C���ƌ����ɂ��ْ��w�E�F�[�u���b�g�x(�����o��)�ɏڂ����������L����Ă��܂��D��G�c�ɂ����ƁC�摜�� | ||||||||
| ���x��(�𑜓x)�@�@�@���� | ||||||||
| �̓�̓����ɕ������܂��D���x�����傫���Ȃ邲�ƂɎ���ɉ摜�̑�܂��ȕ��������o����܂��D�e���x���́C�ߎ������ƂR�̏ڍו����C���Ȃ킿�����C�����C�Ίp�����ɕ�������܂��D | ||||||||
| �@�J�t�F�E�H�[�������摜���C���x��7�܂ŕ������C�}�P�̂Q�s�ڂ̐}�͂��̂������x���Q�C�R�C�S�̐����������ڂ��Ă���܂��D�ő�d���E�F�[�u���b�g����������ƁC�m���ɂ˂���R��̃p�^�[�����J�t�F�E�H�[�������摜�Ɋ܂܂�Ă��邱�Ƃ��킩��܂��D | ||||||||
| �@�}1�̂R�s�ڂ̍����̐}�����x���Q�C�R�C�S�̐������������Z�������̂ł��D���̕����̃f�[�^�����͍����̖{�����܂�ł���̂ł��D���̂��Ƃ��ؖ����邽�߂ɁC���x���Q�C�R�C�S���܂܂Ȃ����������Z���Ă݂܂��傤�D�J�t�F�E�H�[���摜�ɋ߂��}�ł���Ȃ���C�����ɂ͕��s�����X�ނ��Č���������͔������Ă��܂���D | ||||||||
| �@�ő�d���E�F�[�u���b�g�����́C���������f�[�^�����ׂĉ��Z����ƌ��̃f�[�^�Ɗ��S�Ɉ�v����Ƃ������S�č\���������̂ŁC���ǁC�˂���R��̃p�^�[�����܂ރ��x���Q�C�R�C�S�ɍ����̗v�������邱�Ƃ����w�I�Ɏ����ꂽ���ƂɂȂ�܂��D | ||||||||
| 3. ���̑��̌X�������Ƃ˂���R��̃p�^�[���@(�V��E�V��[1]) | ||||||||
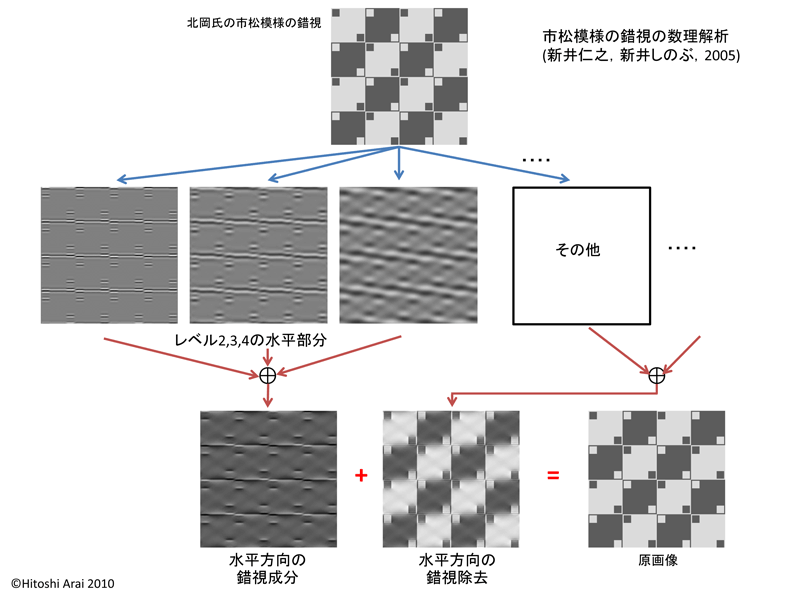
| �J�t�F�E�H�[�������ȊO�̌X�������ɂ��ẮC�ǂ̂悤�ɂȂ�ł��傤���D���낢��ȍ����������Ă݂܂������C�ǂ�����x���Q�C�R�C�S�̐��������ɍ����̗v�����܂܂�Ă��邱�Ƃ��킩��܂����D���̗�Ƃ��āC�����ł͖k���������ɂ��s���͗l�̍����Ɛ��H�̍����Ɋւ����͌��ʂ��q�ׂ܂��D | ||||||||
| �܂��k�����̎s���͗l�����̉�͂���n�߂܂��D �s���͗l�����͐����̐��Ɛ����̐����Ƃ��ɌX���Č���������ł��D�����ł͐��������̍����v���̏��������܂����D����ƁC���摜�̎s���͗l�͂قƂ�ǎc���Ă���ɂ�������炸���������̍����͊m���ɏ�������Ă��܂��D�������c�����̍��������ɂ͑���������Ă��Ȃ��̂ŁC���������̍����͎c�����܂܂ƂȂ�܂� (�}2��3�s�ڒ����̐}�Q��)�D | ||||||||
 |
||||||||
| �}2 | ||||||||
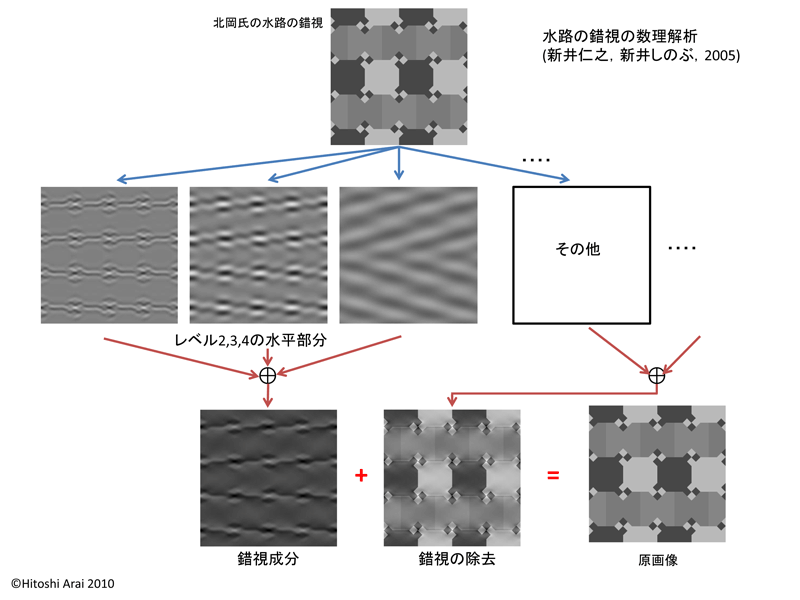
| ���ɖk�����̐��H�̍�������͂��Ă݂܂��傤�D���̏ꍇ���˂���R��̃p�^�[���������̃��x���Q�C�R�C�S�̐��������ɂ���C���ꂪ�����̗v���ɂȂ��Ă��邱�Ƃ����w�I�Ɏ�����܂����D | ||||||||
 |
||||||||
| �}3 | ||||||||
| 4. ���o�̑��I����ƃJ�t�F�E�H�[������ (Arai [2]) | ||||||||
| ���o�n�́C�j���[�����̎�e��ɂ��Ǐ��I�ȏ���̂ق��ɁC���Ƃ��Α�]�玿V1��Ȃǂł́C�j���[�����̐��������ɂ����I�ȏ�����s���Ă��܂��D���̈�Ɏ��̂悤�ȏ��������܂��D | ||||||||
| ���͂ɑ傫�ȃR���g���X�g�̎h��������ꍇ�́C�ア�R���g���X�g�̎h���͗}������C ���͂ɃR���g���X�g�̑傫�Ȏh�����Ȃ��ꍇ�́C�ア�R���g���X�g�̎h���͋��������D | ��������u�R���g���X�g�m�o�̖@���v�ƌĂԂ��Ƃɂ��܂� | |||||||
| ���̂悤�Ȃ��Ƃ����ۂɎ��o�ŋN���Ă��邱�Ƃ������V���������C�Ȃ�тɂ��̏���̐������f�����ɂ��Ă͎Q�l������Arai[2]���Q�Ƃ��Ă��������D | ||||||||
| ���̑��I�������J�t�F�E�H�[�������̎��o����ɂǂ̂悤�ȉe����^���Ă���̂��ׂ邱�Ƃɂ��܂��傤�D | ||||||||
| ���̂��߂� Gregory�炪�����������̌��ۂɒ��ڂ��܂��D�ނ�͏�f�̘_�� {GH]�ɂ����ăJ�t�F�E�H�[�������̐������ɂ��āC���̂悤�Ȃ��Ƃ��w�E���܂����D | ||||||||
| �@�@�������̐F���J�t�F�E�H�[���摜�ɂ��鍕���^�C����荕�����C���邢�@�@�͔����^�C����蔒���ƍ������Ȃ��Ȃ�D | ||||||||
| �A�@�������̑����������ƍ������Ȃ��Ȃ�D | ||||||||
| �܂� �@ �̉�͂���n�߂܂��D�}4���������̐��������^�C����荕�������}�ŁC�}4�E�̓J�t�F�E�H�[�������摜�ł��D�m���ɐ}4���ł͌X���̍������N�����Ă��Ȃ����Ƃ��킩��܂��D | ||||||||
|
|
||||||||
| �}4 | ||||||||
| �����Ő}4���̉摜�̍ő�d���E�F�[�u���b�g�ɂ�镪���̂����C�������̐������������邱�Ƃɂ��܂��傤�D�D | ||||||||
 |
||||||||
| �}5 | ||||||||
| �������˂���R�̃p�^�[���Ƃ��Ă͕s�\���Ȃ��̂ƍl�����܂��D���Ƃ��ΊԂ����f����Ă��܂��D���I�����łǂ̂悤�ȏ�v�Z�����̂��𒊏o����Ɛ}6�̂悤�ɂȂ�܂��D | ||||||||
 |
||||||||
| �}6 | ||||||||
| �}6�E���J�t�F�E�H�[�������摜�̏ꍇ�ł��D����`�����ɂ���Ă��ׂ��˂���R��̃p�^�[��������܂��D����C�������������^�C����荕���ꍇ���}6���ŁC���̏ꍇ�C�˂���R��̃p�^�[���͖��炩�Ɍ���܂���D�Ȃ�����͏����ɑ��I����݂̂ɂ����ʂ��o�������̂ł��D���������āC���̂悤�ȃp�^�[�������摜�ɂ�������ƌ����Ă��邱�ƂɂȂ�܂����C���ۂɌ��摜���悭����Ƃ��̂��Ƃ��m�F�ł��܂��D | ||||||||
| ���ɇA�ɂ��ĉ�͂��܂����C����ɂ����I�����̐������f��������ɋ����[�����Ƃ����炩�ɂȂ�܂��D | ||||||||
|
�@Earle and Maskell (1993) �ɂ��ƁC�J�t�F�E�H�[�������̐����̊D�F�̐������L������ƁC�������̌X�����t�ɂȂ�܂��D����ɂ��̘_���ɂ́C�R�����̎w�E�Ƃ������ƂŁC�˂���R��̖��Ì��ۂ������̊D�F�̑т̒��Ɍ���Ă���C����̓t���[�U�[�̂˂���R�Ƌt�����ɂȂ��Ă��āC�^�C���̃G�b�W���܂܂Ȃ��ƋL����Ă��܂��D���̌��ۂ͂��́C�������f�����������I����ɂ���ċN���邱�Ƃ��v�Z�ɂ�莦�����Ƃ��ł���̂ł��I�}6���������������D |
||||||||
 |
||||||||
| �}6 | ||||||||
| �}6�E�����摜�C�}6�������I�����ɂ��v�Z���ʂ𒊏o�������̂ł��D�m���ɑ��I�����ŋt�����̂˂���R���v�Z����Ă��邱�Ƃ��킩��܂��D���ꂪ��L�̌��ۂ��������郁�J�j�Y���ł��D | ||||||||
| �ȏ�q�ׂĂ����悤�ɁC���w����g����C�����ɑ��Ă���܂łƂ͈�����^�C�v�̐V������͂��s�����Ƃ��ł��܂��D | ||||||||
| �@���w�I�Ȑ����ȂǁC�ڂ������Ƃ͉��L�̘_���C�V��E�V��[1] ��Arai [2] �ɂ���܂��̂ŁC�ǂ����������������D����ɃE�F�[�u���b�g��i���������u��������܃t���[�����b�g�v(�V��E�V��)�ɂ��w�I�����̉�͂ɂ��ẮC�V��E�V��[3]�C[4]���Q�ƁD | ||||||||
|
|
||||||||
| �Q�l���� | ||||||||
| [1] �V��m�V�C�V�䂵�̂ԁC�E�F�[�u���b�g�����Ō���C�����̌X�������ɂ�����ގ����CVISION, J. Vision Soc. of Japan, 17 (2005), 259-265. | ||||||||
| [2] H. Arai, A nonlinear model of visual information processing based on discrete maximal overlap wavelet,Interdisciplinary Information Sciences 11 (2005), pp. 177-190. | ||||||||
| �lj������i2015/12/9�j | ||||||||
| [3] �V��m�V�C�V�䂵�̂ԁC�����̐������f���ƍ����}�`�̍\����́CJapanese Psychological Review, vol. 55, no. 3, pp. 309-333 (2012). | ||||||||
| [4] H. Arai and S. Arai, Framelet analysis of some geometrical illusions, Japan. J. Indust. Appl. Math. vol. 27, no. 1, pp. 23-46 (2010). | ||||||||
|
|
||||||||
| ���̃y�[�W�̒��쌠�͐V��m�V�ɂ���܂��D�{�y�[�W�ɋL�ڂ̓��e�E�摜�̈ꕔ���邢�͑S���̖��f�]�ڂ��ւ��܂��D | ||||||||
|
|
||||||||
| �����̉Ȋw�ق̊O������A�N�Z�X���Ă�����́C�����N���b�N���Ă��������D�����̉Ȋw�ٓ����ł� | ||||||||
 |
||||||||
